Class 11- Chapter 6 - Work Energy And Power

 

WORK, ENERGY AND POWER

Contents

1. Overview
      Definition of Work
2. Elaborations 
3.Definition of Energy
         Kinetic Energy
         Potential Energy          
4.Elaborations  
5.Definition of Power
     Definition of Work Energy Theorem
     Law on the Conservation of Energy
     Energy cannot be Produced or Lost
     Mass and Energy Equivalence 
     Law on the Conservation of Energy
     Energy cannot be Produced or Lost
     Mass and Energy Equivalence 
6.  Elaborations 
 7.  Collision
     Elastic Collisions
     Inelastic Collisions
8. Elaborations 
9.Elastic Collision in One dimension
10.Elastic Collision in One dimension
12.Conservative and on-conservative forces
        Conservative forces
        Non-conservative forces
        Non-conservative forces
        Example Questions
Important Extra Questions 
NCERT- Q&A -SOLUTIONS
13.Very Short Answer Type
14.Very Very Short Answer Type
15 Long Answer Type
16. Numerical Problems
17.Value-Based Type 

1

Overview

Here is a quick overview of some of the important basics of work, energy and power. 

Definition of Work

Definition	When a force applied to an object moves that object, then it is called as Work
Formula	W = F × d
SI Unit	The SI unit of work is labelled as joule (J).

Definition of Energy

Definition	Energy is defined as the capacity to do work.
Formula	P.E. = mgh
Si Unit	The SI unit of energy is called as joules (J)

Definition of Power

Definition	The rate at which work is done i.e. the energy converted can be defined as Power.
Formula	P = W/t
SI Unit	The SI unit of power is called watt (W).

Definition of Work  

 Work is said to be achieved as a movement of a  body or entity is caused by the use of external force. Work is also interpreted as an action in the direction of the applied force. 

W = F × d

For example, a force of 40 Newtons (N) that moves the object 5 metres in the same direction as the force does 200 Joules (J) of work.

The SI unit of work is taken as joule (J). 

Example

An object is pulled across the surface by a 100 N force which is acting parallel to the surface horizontally. Calculate the amount of work done which is performed by the force in the moving object through a distance of 8 m

Solution: 

Given, F = 100 N
d = 8 m
Since F and d are present in the same direction,
θ = 0, [θ is the angle of the force to the direction of movement]W = F Cos θ
= 100 x 8 x Cos 0
= 800 J [Since Cos 0 = 1]

2

Elaborations:

WORK

• The work done by the force is defined to be the product of component of the force in the direction of the displacement and the magnitude of this displacement.
• The work and energy have the same dimensions [ML-2 T-2]
• The SI unit is joule (J).

Work done by a constant force

The work done by the constant force F , is given by

• W = F.d cosθ
•  W =F.d, when θ = 0⁰
•  W = - F.d, when θ = 180⁰ 
• W =0, when θ = 90⁰
• So, Work done can be zero, positive or negative

Special cases

• If ϴ=0, then maximum work is done given by W =Fd .
• If ϴ=900, then work done =0
• If ϴ is between 00 and 900, the work done is positive.
• If ϴ is between900 and 1800, the work done is negative.

Situations in which Work done = 0 as the displacement is zero (d=0):

• A weightlifter holding a 150 kg mass steadily on his shoulder for 30 s does no work on the load during this time.

the force is zero (F=0):

• A block moving on a smooth horizontal table is not acted upon by a horizontal force (since there is no friction), but may undergo a large displacement

the force and displacement are mutually perpendicular (ϴ = 900)

• For the block moving on a smooth horizontal table, the gravitational force mg does no work since it acts at right angles to the displacement.

Situations in which work done is negative

• A ball is thrown in the upward direction – work done by the gravitational force is negative.
• The work done by the frictional force, when we push the book to a distance is negative
• The work done by the gravitational force, when we are lifting a bucket of water from the well is negative

PROBLEM

• A cyclist comes to a skidding stop in 10 m. During this process, the force on the cycle due to the road is 200 N and is directly opposed to the motion.

1. How much work does the road do on the cycle?
2. How much work does the cycle do on the road ?

Solution

1. Work done on the cycle by the road = the work done by the frictional force on the cycle.

• Here ϴ =1800, F=200N, d=10m ,thus W = Fd cos ϴ = 200 x 10 x cos1800 = -2000J

1. The magnitude of the force on the road due to cycle is 200 N.

• The displacement of the road = 0.
• Thus, work done by cycle on the road is zero.

Force –Displacement graph (F-d Graph)

• A graph drawn with displacement along X –axis and force along Y- axis.
• Area under F-d graph gives the work done.

F-d graph of work done by a constant force

F-d graph of work done by a uniformly varying force

WORK DONE BY A VARIABLE FORCE

• The F-d graph of a varying force in one dimension, is given by

• For a small displacement Δx, the force F(x) is almost constant.
• Thus, the work done is

• Therefore, the total work done is given by

• Or , if Δx → 0, then

PROBLEM

A woman pushes a trunk on a railway platform which has a rough surface. She applies a force of 100 N over a distance of 10 m. Thereafter, she gets progressively tired and her applied force reduces linearly with distance to 50 N. The total distance through which the trunk has been moved is 20 m.

1. Plot the force applied by the woman and the frictional force which is 50 N.
2. Calculate the work done by the two forces

over 20 m.

Solution

1. The graph is

1. The work done by the women is WF= Area of rectangle ABCD + area of the trapezium CEID

NB: The area of trapezoid is given by

A=  x (a + b) x h

3

Definition of Energy

 Energy is defined as the ability to do a task. 

Energy cannot be produced or lost. It can only be converted from one type to the next. The Energy Unit is much like the Job Unit, i.e. It’s Joules. 

P.E. = mgh

Most forms of energy seem to be either kinetic or potential. The energy of action is defined as kinetic energy, while the potential energy is the energy contained in the body and determined by the amount of work performed.

The SI unit of energy is called joules (J).

Kinetic Energy  

Energy generated by the body because of its motion is regarded as the kinetic energy of the body. Kinetic energy acquired by moving the body is equivalent to average work performed by the body just before heading to rest. 

Kinetic energy = 1/2 mv² 

Potential Energy  

Potential Energy  is defined as the Energy which is generated on or by a body as a result of its position ,configuration or state . 

                                   P.E. = mgh

 This Energy generated is stored in the system or a body. Examples for potential energy can be cited as Energies like gravitational potential energy, electrostatic potential energy, elastic potential energy etc.

4

Elaborations:

ENERGY

• Energy is the capacity for doing work.
• It can be measured by the work that the body can do.
• Joule is the SI unit of energy.

Alternative units of Work /Energy

erg	10-7J
electron volt (eV)	1.6 x 10-19 J
calorie (Cal)	4.186 J
kilowatt hour (kWh)	3.6 x 106 J

MECHANICAL ENERGY

• The energy of an object due to its motion or position.
• Total mechanical energy is the sum of kinetic and potential energy

KINETIC ENERGY

• The kinetic energy of an object is a measure of the work an object can do by the virtue of its motion
• Kinetic energy an object of mass m moving with velocity v, is

• Kinetic energy is a scalar quantity.
• In terms of momentum , p

• The dimensions are [ML2T-2]
• The SI unit is joule (J).

WORK- ENERGY THEOREM FOR A CONSTANT FORCE

The change in kinetic energy of a particle is equal to the work done on it by the net force

Proof

• We have , v2 –u2 =2ad ,
• Where u – initial velocity , d – displacement, v – final velocity
• Multiplying both sides by m/2,

• In general

• This is known as work-energy theorem

POTENTIAL ENERGY

• Potential energy is the ‘stored energy’ by virtue of the position or configuration of a body.
• Energy in a stretched string is an example.
• The potential energy is released in the form of kinetic energy.
• It is a scalar quantity.
• The dimensions of potential energy are [ML2T-2].
• The SI unit is joule (J).

Gravitational Potential Energy (V)

• Gravitational potential energy of an object at a height h, is the negative of work done by the gravitational force in raising the object to that height.

• The gravitational force can be written as

• Thus, the gravitational force F equals the negative of the derivative of V(h) with respect to h.
• The negative sign indicates that the gravitational force is downward.

Show that the gravitational potential energy of the object at height h, manifests itself as kinetic energy of the object on reaching the ground.

Proof

• The speed of an object released from a height h, when it just hits the ground is given by

• Multiplying this equation with m/2 on both sides

• Thus the kinetic energy = gravitational potential

energy.

5 Definition of Power

  Power is a physical phenomenon with a variety of different interpretations, out of which the most popular one describes power  as follows.. The rate at which work is performed is known as work. This is the measure of Energy consumed per unit of time.

P = W/t
Where,
P = Power
W = Work done
T = Time taken

Definition of Work Energy Theorem

The work done on a body by applying force is equal to the change in kinetic energy of the body. This is defined as Work-Energy Theorem. 

Law on the Conservation of Energy 

The Law of Conservation of Energy states that the total energy of an isolated system does not alter or change. Energy can be converted from one form to another, but the total energy that is present in an independent entity remains unchanged. 

Energy cannot be Produced or Lost

In addition to mechanical energy, energy can manifest itself in many other ways. Any of these forms include: thermal energy, electrical energy, chemical energy, visual light energy, nuclear energy, etc. 

Mass and Energy Equivalence 

Equivalence of mass and energy is an important section of this chapter.. According to Albert Einstein, Energy and mass are synonymous. That is, mass can be transformed into energy, and energy can be transformed into mass.

6

Elaborations:

PRINCIPLE OF CONSERVATION OF MECHANICAL ENERGY

• The total mechanical energy of a system is conserved if the forces, doing work on it, are conservative.
• If forces are conservative

K + V = constant

Proof

• If a body undergoes displacement Δx , under the action of conservative forces, F(x), from work – energy theorem,

ΔK=F(x) Δx

• The change in potential energy is given by

ΔV = -F(x)Δx

• Adding the two equations

ΔK+ΔV= F(x) Δx – F(x) Δx = 0

Δ(K+V) = 0

K+V = constant

Conservation of Mechanical Energy in a Freely Falling Body

• Consider a ball of mass m being dropped from a cliff of height h.

Total Energy at the point A

• Kinetic energy at A is zero (K=0), since v=0
• Potential energy at A is , V = mgH
• Thus total energy at A, is

E=K+V =0+mgH =mgH

Total Energy at the point B

• Kinetic energy at B is

But we have

• Thus

• Potential energy at B is , V = mgh
• The total energy at B is

E=K+V =mg(H -h)+mgh =mgH

Total Energy at the point C

• The kinetic energy at C is

• But we have

v2 -02 = 2gH

v2 = 2gH

• Thus
• 
• The potential energy at C is, V = 0
• The total energy at C
• E=K+V =mgH +0=mgH
• Therefore total energy at A = total energy at B = Total energy at C = mgH = a constant

Graph of the variation of kinetic energy and potential energy of a freely falling body

7

THE POTENTIAL ENERGY OF A SPRING

• The work done by an external force to compress or extend a spring is stored as the potential energy in it.

Spring Force (Fs)

• The restoring force developed in a spring ,when a force is applied on it is called spring force.
• The spring force is a variable force which is conservative.

Force law of spring ( Hooke’s law )

• In an ideal spring, the spring force Fs is proportional to the displacement.

Fs =-kx

• Where k – spring constant
• Unit of spring constant is N/m.
• The negative sign shows that spring force is opposite to the displacement.

Spring is stiff – k is large

Spring is soft – k is small.

Equation for the potential energy of a spring

Integration method

The work done by the spring force for an extension of xm is

• Thus, work done by the applied force will be

• Therefore, this work done is stored as the potential energy in the spring.
• Potential energy of spring is

ii) Graphical method

• The force – displacement graph of the spring is

• Area under the graph = work done by the spring force
• Thus

• Thus, work done by the applied force is

PROBLEM

An elevator can carry a maximum load of 1800 kg (elevator + passengers) is moving up with a constant speed of 2 m s–1. The frictional force opposing the motion is 4000 N. Determine the minimum power delivered by the motor to the elevator in watts as well as in horse power.

Solution

• Downward force on the elevator is

• The power is

 

8

Collision

Collision is characterised as an isolated occurrence in which two or more colliding objects exercise relatively strong forces over a relatively short period of time. The collision between particles has been widely categorised into two forms which can be defined as: 

• Elastic Collisions
• Inelastic Collisions

Elastic Collisions 

A collision between two particles or bodies is considered to be elastic if both the linear momentum and the kinetic energy of the system are preserved is said to be known as Elastic Collisions. Ex: a collision between atomic particles, electrons, marble balls and billiard balls.

Inelastic Collisions 

A collision is considered to be an inelastic collision if the linear momentum of the system is retained, but the kinetic energy is not maintained.

Elaborations:

COLLISIONS

• A collision is an isolated event in which, two or more bodies exert strong forces on each other for a short time.

Types of collisions

Elastic collisions

• The momentum and kinetic energy are conserved.
• It is an ideal collision.

Completely inelastic collisions

• Collision in which the two particles move together after the collision.
• The momentum is conserved, but kinetic energy is not conserved

Inelastic collision

• The momentum is conserved, but kinetic energy is not conserved.
• Most of the collisions are inelastic.

One dimensional collision ( head- on collision )

• Velocity of particles before collision and after collision is directed along the same straight line.

Two dimensional collision

• Velocities of particles lie in a plane.

9
ELASTIC COLLISION IN ONE DIMENSION

• Dividing equations (4) and (3)

On simplification

Thus the relative velocity after collision is numerically equal to relative velocity before collision.

• Similarly

Special cases

i) If m2 is initially at rest ( u2 = 0), then

ii) If m1 = m2 = m

Thus, the velocities are exchanged.

iii) If m1 = m2 = m and u2 = 0

• Thus the first body comes to rest and second body attains the velocity of the first body

COMPLETELY INELASTIC COLLISION IN ONE DIMENSION

• Substituting for vf ,

Thus change in kinetic energy is a positive quantity.

10

COLLISIONS IN TWO DIMENSIONS

• In a two dimensional collision momentum along x and y direction should be conserved.

11 Example Questions

Here are a few important examples of  questions to make you thorough in the chapter.

1. Comets are passing around the sun in extremely elliptical orbits. The gravitational force on the comet due to the sun is not natural to the velocity of the comet in general. Yet the function of gravitational force over a full orbit of the comet is negligible. Why? 

Ans. The force of gravity is defined as a conservative force. The work undertaken by conservative forces on a closed path is zero. Thus, for a full orbit of the comet, the work undertaken by the gravitational force is zero.

2. A molecule with a speed of 300 m s-1 hits the wall of the container at an angle 40∘ with the normal and rebounds with the same speed. During the collision is the momentum conserved?

Ans. The collision can be defined as an elastic collision. Whether the collision is an elastic or an inelastic collision, the momentum is conserved. The molecule travels at a speed of 300 m/s and strikes the wall and rebounds with the same speed. Therefore, the rebound velocity is zero. During the collision, the total kinetic energy is conserved.

12 Conservative and non-Conservative Forces  

Conservative Force

• A force is conservative if

1. it can be derived from a scalar quantity V(x).
2. the work done by the force depends only on initial and final positions.

• Examples are, gravitational force, electric force , spring force etc
• The work done by a conservative force in a closed path is zero.
• The change in potential energy of a conservative force is equal to the negative of the work done by the force.

Show that the work done by a conservative force depends only on end points.

• If the force F(x) is conservative, we can write

• Thus

• Therefore work done depends only on end points.

Non conservative forces

• The forces in which the work done depends on the factors like velocity or path taken.
• Example: frictional force, viscous force etc.

Problem:

An elevator can carry a maximum load of 1800 kg (elevator + passengers) is moving up with a constant speed of 2 m s–1. The frictional force opposing the motion is 4000 N. Determine the minimum power delivered by the motor to the elevator in watts as well as in horse power.

Solution

• Downward force on the elevator is

• The power is

NCERT- Q&A -SOLUTIONS

13 Very Short Answer Type

Question 1.
The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative:

1. work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket,
2. work done by the gravitational force in the above case,
3. work done by friction on a body sliding down an inclined plane,
4. work done by an applied force on a body moving on a rough horizontal plane with uniform velocity,
5. work done by the resistive force of air on a vibrating pendulum in bringing it to rest.

Answer:
1. We know that: W = F→,S→ = FS cos θ
‘Positive’
Reason: Force is acting in the direction of displacement (θ = 0°)
2. ’Negative’
Reason: Force is acting in the opposite direction to displacement (θ =180°)
3. ’Negative’
Reason: Force of friction is opposite to the displacement (θ = 180°)
4. ‘Positive’
Reason: The body mover in the direction of force applied (θ = 0°)
5. ‘Negative’
Reason: The resistive force opposes the motion (θ = 0°)

Question 2.
A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with coefficient of kinetic friction = 0.1. Compute the
(a) work done by the applied force in 10 s
(b) work done by friction in 10 s
(c) work done by the net force on the body in 10 s
(d) change in kinetic energy of the body in 10 s and interpret your results.
Answer:
Here M = 2 kg; u = 0; μ= 0.1; applied force, F = 7N, t = 10s
Force of friction, f= μMg = 0.1 x 2 x 9.8 = 1.96 N
.’. net force under which body moves, F’ = F- f = 7 – 1.96 = 5.04 N

Question 3.
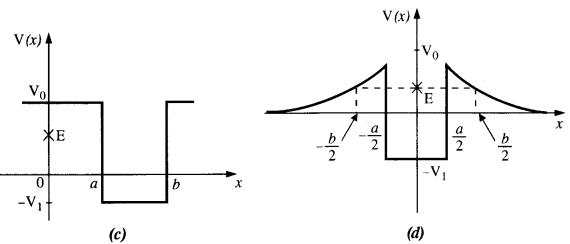
Given in Fig. are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.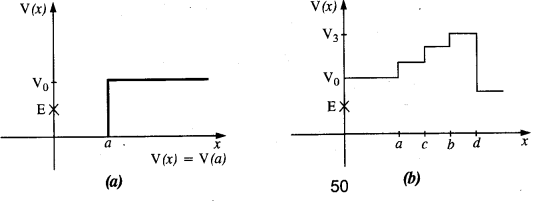


Answer:
(a) We know that Total energy E = KE + PE, kinetic energy can never be negative. In the region between x = 0 & x = a.
Potential energy is ‘0’. So, kinetic energy y is positive. In region x > a the potential energy has a value greater than ‘E’. So kinetic energy will be negative in this region. Hence the particle cannot be present in the region x > a.

(b) Here PE > E, the total energy of the object and as such the kinetic energy of the object would be negative. Thus object cannot be present in any region on the graph.

(c) Here x = 0 to x = a & x > b, the P E is more then E so, K E is negative. The particle cannot be present in these portions.

(d) The object cannot exist in the region between
x = −b2 to x = −a2 & x = −a2 to x = −b2
Because in this region P E > E.

Question 4.
The potential energy function for a particle executing linear simple harmonic motion is given by V (x) = Kx2 /2, where A is the force constant of the oscillator. For A = 0.5 N nr1, the graph of V (x) versus x is shown in Fig. Show that a particle of total energy 1 J moving under this potential must ‘turn back’ when it reaches x = ± 2 m.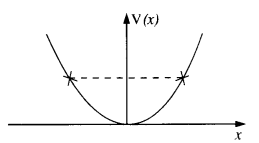

Answer: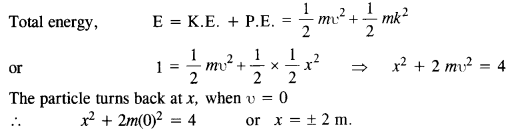

Question 5.
Answer the following :
(a) The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained? The rocket or the atmosphere ?
(b) Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet’s velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why?
(c) An artificial satellite orbiting the earth in very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the earth ?
(d) In Fig.

1. The man walks 2 m carrying a mass of 15 kg on his hands. In Fig.
2. He walks the same distance pulling the rope behind him. The rope goes over a, pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater ?
   

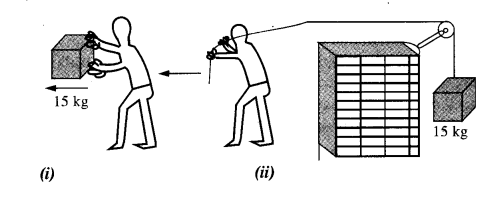
Answer:
(a) Heat energy required for the burning of the casing of a rocket is obtained by a rocket. Since the work is done against the friction, the kinetic energy of the rocket decreases continuously and this work against friction reappears as heat energy.

(b) This is because of the conservative nature of the gravitational force. Work done by the gravitational force in a closed path is zero.

(c) As an artificial satellite gradually loses its energy due to dissipation against atmospheric resistance, its potential decreases rapidly. As a result, the kinetic energy of the satellite slightly increases i.e. its speed increases progressively.

(d) In fig (i) the force applied by the man is perpendicular to the direction of movement of mass, i.e. θ = 90°
W = Fs cos θ = Fs cos 90° = 0
In figure (ii) the force applied is in direction of the movement of mass i.e. θ = o°
∴ W = Fs cos θ
= Mgs cos θ
= 15 × 9.8 × 2 × 1
= 294 J.

Question 6.
Underline the correct alternative:
(a) When a conservative force does positive work on a body, the potential energy of the body increases/decreases/ remains unaltered.
(b) Work done by a body against friction always results in a loss of its kinetic/potential energy.
The rate of change of total momentum of many-particle system is proportional to the external force/sum of the internal forces on the system.
(c) In an inelastic collision of two bodies, the quantities which do not change after the collision are the total kinetic energy, total linear momentum, and total energy of the system of two bodies.
Answer:
(a) Work done by conservative force is equal to the negative of potential energy. When work done is positive, potential energy decreases.
(b)  Kinetic energy, because friction does work against motion of the body.
(c) External force, because in many-particle systems, the internal forces in the system cancel each other and hence cannot change the net momentum of the system.
(d) In inelastic collision, total energy and linear momentum are conserved. However, kinetic energy decreases.

Question 7.
State if each of the following statements is true or false. Give reasons for your answer.

1. In an elastic collision of two bodies, the momentum and energy of each body are conserved.
2. The total energy of a system is always conserved, no matter what internal and external forces on the body are present.
3. Work done in the motion of a body over a closed loop is zero for every force in nature.
4. In an inelastic collision, the final kinetic energy is always less than the initial kinetic energy of the system.

Answer:

1. False, the momentum and energy of each body are conserved.
2. False, the external force on the system may increase or decrease the total energy of the system.
3. False, for the non-conservative forces (friction) the work done in closed-loop is not zero.
4. True, usually in an inelastic collision the final kinetic energy is always less than the initial kinetic energy of the system.

Question 8.
Answer carefully, with reasons :
(a) In an elastic collision of two billiard balls, is the total kinetic energy conserved during the short time of collision of the balls (i.e., when they are in contact) ?
(b) Is the total linear momentum conserved during the short time of an elastic collision of two balls ?
(c) What are the answers to (a) and (b) for an inelastic collision ?
(d) If the potential energy of two billiard balls depends only on the separation distance between their centers, is the collision elastic or inelastic ? (Note, we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy).
Answer:
(a) In this case total kinetic energy is not conserved because when the bodies are in contact during elastic collision even, the kinetic energy is converted into internal energy.
(b) Yes, because total momentum conserves as per law of conservation of momentum.
(c) In inelastic collision, K.E. is not conserved but linear momentum is conserved.
(d) It is a case of elastic collision because in this case the forces are of conservative nature

Question 9.
A body is initially at rest. It undergoes one-dimensional motion with constant acceleration. The power delivered to it at time t is proportional to
(1) tm
(2) t
(3) t3/2
(4) t2
Answer: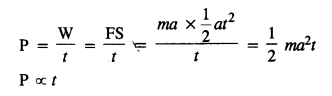

Question 10.
A body is moving uni-directionally under the influence of a source of constant power. Its displacement in time t is proportional to
(1) tm
(2) t
(3) t3/2
(4) f2
Answer:

Question 11.
A body constrained to move along the z-axis of a coordinate system is subject to a constant force F given by F⃗ = i^+2j+3K
where i^+j+Kare unit vectors along the x-, y- and z-axis of the system respectively. What is the work done by this force in moving the body a distance of 4 m along the z-axis ?
Answer: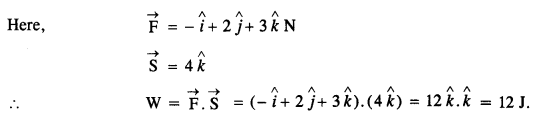

Question 12.
An electron and a proton are detected in a cosmic ray experiment, the first with kinetic energy 10 keV, and the second with 100 keV. Which is faster, the electron or the proton? Obtain the ratio of their speeds, (electron mass = 9.11 x 10-31 kg, proton mass = l.67 x 10-27 kg, 1 eV = 1.60 x 10-19 J).
Answer:
Let υe = Speed of electron
υp = speed of the proton
mg = mass of electron
and mp = mass of proton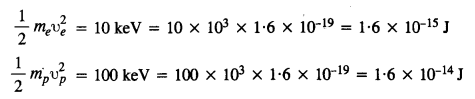

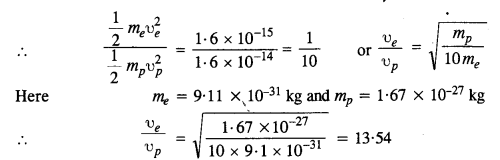
Question 13.
A rain drop of radius 2 mm falls from a height of 500 m above the ground. It falls with decreasing acceleration (due to viscous resistance of the air) until at half its original height, it attains its maximum (terminal) speed, and moves with uniform speed thereafter. What is the work done by the gravitational force on the drop in the first and second half of its journey ? What is the work done by the resistive force in the entire journey if its speed on reaching the ground is 10 ms-1?
Answer: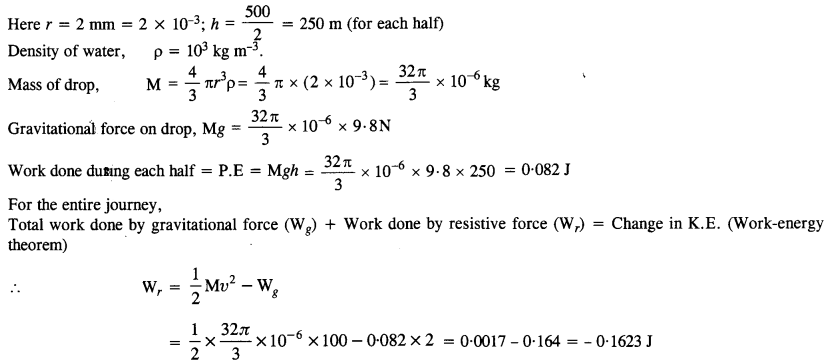

Question 14.
A molecule in a gas container hits a horizontal wall with speed 200 ms-1 and angle 30° with the normal, and rebounds with the same speed. Is momentum conserved in the collision ? Is the collision elastic or inelastic ?
Answer:
In all types of collisions, momentum is conserved. Let us check the conservation of kinetic energy.As the wall is too heavy, the recoiling molecule produces no velocity in the wall. l%m is mass of the gas molecule and M is mass of wall, then total K.E. after collision,

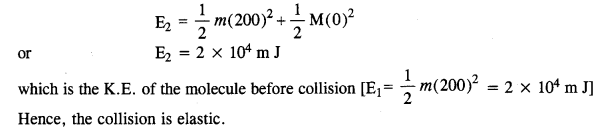
Question 15.
A pump on the ground floor of a building can pump up water to fill a tank of volume 30 m3 in 15 min. If the tank is 40 m above the ground, and the efficiency of the pump is 30%, how much electric power is consumed by the pump ?
Answer: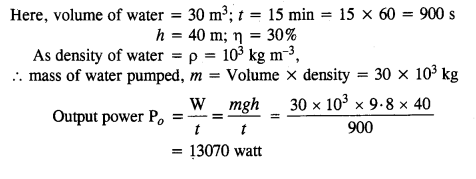

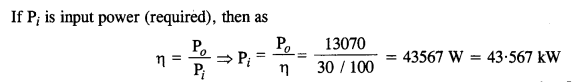
Question 16.
Two identical ball bearings in contact with each other and resting on a frictionless. table are hit head-on by another ball bearing of the same mass moving initially with a speed V. If the collision is elastic, which of the following (Fig.) is a possible result after collision ?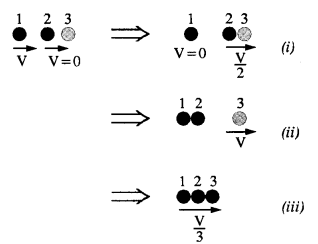

Answer:
Collision is elastic, so K.E. of the system is conserved.

Question 17.
The bob A of a pendulum released from 30° to the vertical hits another bob B of the same mass at rest on a table as shown in Fig. How high does the bob A rise after the collision? Neglect the size of the bobs and assume the collision to be elastic.
Answer: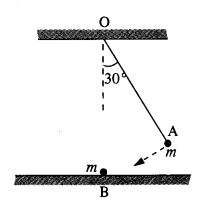

Since the collision is elastic, therefore A would come to rest and B would begin to move with the velocity of A to conserve the linear momentum.

Question 18.
The bob of a pendulum is released from a horizontal position A as shown in Fig. If the length of the pendulum is 1.5 m, what is the speed with which the bob arrives at the lowermost point B, given that it dissipated 5% of its initial energy against air resistance ?
Answer: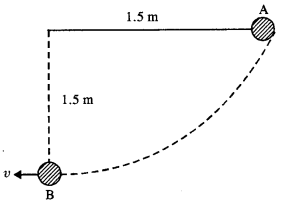

P.E. of the bob at position A = mgh = m x 9.8 x 1.5
Since 5% of energy is lost when reach at B, so K.E. at the lowermost point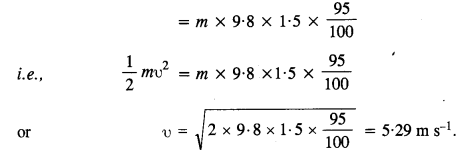

Question 19.
A trolley of mass 300 kg carrying a sandbag of 25 kg is moving uniformly with a speed of 27 km/h on a frictionless track. After a while, sand starts leaking out of a hole on the trolley’s floor at the rate of 0.05 kgs_1. What is the speed of the trolley after the entire sandbag is empty ?
Answer:
The system of trolley and sandbag is moving at a uniform speed. Clearly, the system is not being acted upon by external force. If the sand leaks out, even when no external force acts. So there shall no change in the speed of the trolley.

Question 20.
A particle of mass 0.5 kg travels in a straight line with velocity υ = ax3/2, where a = 5 m-1/2 s-1. What is the work done by the net force during its displacement from x = 0 to x = 2m?
Answer:
Here m = 0.5 kg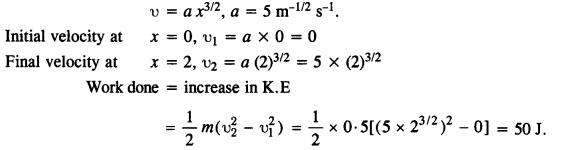

Question 21.
The blades of a windmill sweep out a circle of area A.
(a) If the wind flows at a velocity v perpendicular to the circle, what is the mass of the air passing through it in time t ?
(b) What is the kinetic energy of the air ?
(c) Assume that the windmill converts 25% of the wind’s energy into electrical energy, and that A = 30 m2, υ= 36 km/h and the density of air is 1.2 kg m-3. What is the electrical power produced ?
Answer:
(a) Volume of wind flowing per sec = Aυ
Mass of wind flowing per sec = Aυp
Mass of air passing in time t = Aυpt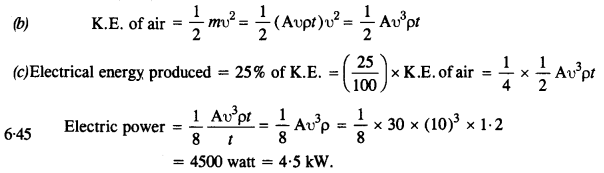

Question 22.
A person trying to lose weight (dieter) lifts a 10 kg mass 0.5 m, 1000 times. Assume that the potential energy lost each time she lowers the mass is dissipated,
(a) How much work does she do against the gravitational force ?
(b) Fat supplies 3.8 x 107 J of energy per kilogram which is converted to mechanical energy with a 20% efficiency rate. How much fat will the dieter use up ?
Answer:
Here m = 10 kg, h = 0.5 m, n = 1000
(a) Work done against gravitational force = W = n mgh
= 1000 x (10 x 9.8 x 0.5)
= 49000 J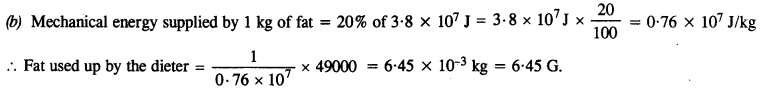

Question 23.
A large family uses 8 kW of power,
(a) Direct solar energy is incident on the horizontal surface at an average rate of 200 W per square meter. If 20% of this energy can be converted to useful electrical energy, how large an area is needed to supply 8 kW?
(b) Compare this area to that of the roof of a house constructed on a plot of size 20 m x 15 m with a permission to cover upto 70%.
Answer:
(a) Energy incident per square meter = 200 W
Let A be the area needed to supply 8 kW
.’. Energy incident on area A = (200 A) W
Energy converted into useful electrical energy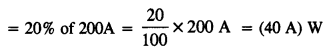

Question 24.
A bullet of mass 0.012 kg and horizontal speed 70 ms-1 strikes a block of wood of mass 0.4 kg and instantly comes to rest with respect to the block. The block is suspended from the ceding by means of thin wires. Calculate the height to which the block rises. Also, estimate the amount of heat produced in the block.
Answer:
By using law of conservation of momentum,
m1u1+ m2u2 = (m1 +m2)υ

Question 25.
Two inclined frictionless tracks, one gradual and the other steep meet at A from where two stones are allowed to slide down from rest, one on each track (Fig.). Will the stones reach the bottom at the same time ? Will they reach there with the same speed ? Explain. Given θ1 = 30°,θ2 = 60°, and h = 10 m, what are the speeds and times taken by the two stones?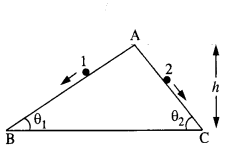

Answer:
Here, K.E. at bottom = P.E. at top

Since vertical height of both planes is same, so they will reach the bottom with same speed. Acceleration of a body sliding down an inclined plane, a = g sin θ
Let t be the time taken by stone 1 to travel AB distance.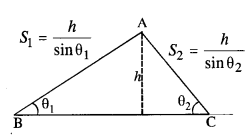

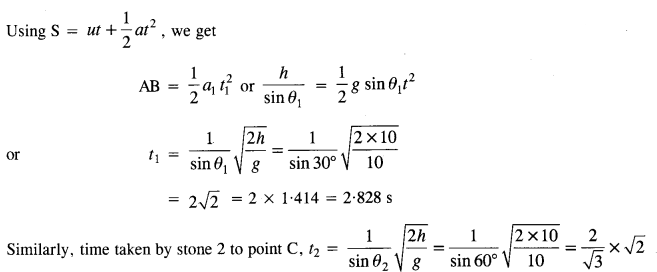
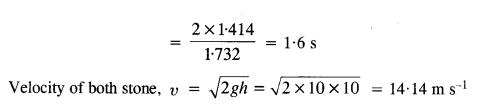
Question 26.
A 1 kg block situated on a rough incline is connected to a spring of spring constant 100 N m-1 as shown in Fig. The block is released from rest with the spring in the unstretched position. The block moves 10 cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has negligible mass and the pulley is frictionless.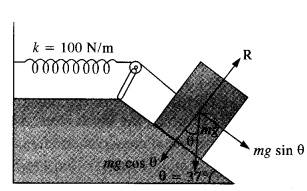

Answer:
From fig, R = mg cos θ
Force of friction, F = μR = μ mg cosθ
Net force on the block down the incline
= mg sinθ – F = mg sinθ – (a mg cosθ = mg (sinθ – μcos θ)
Distance moved, x = 10 cm = 0.1 m
In equilibrium, Work done = P.E. of stretched spring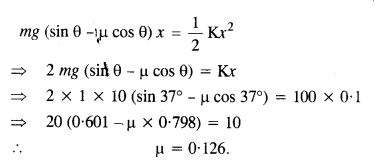

Question 27.
A bolt of mass 0.3 kg falls from the ceiling of an elevator moving down with a uniform speed of 7 ms-1. It hits the floor of the elevator (length of the elevator = 3 m) and does not rebound. What is the heat produced by the impact ? Would your answer be different if the elevator were stationary ?
Answer:
Potential energy of bolt = mgh = 0.3 × 9.8 × 3 = 8.82 J.
Since the bolt does not rebound, the while energy is converted into heat. Since the value of acceleration due to gravity is the same in all inertial systems, the answer will not change even if the elevator is stationary.

Question 28.
A trolley of mass 200 kg moves with a uniform speed of 36 km/h on a frictionless track. A child of mass 20 kg bins on the trolley from one end to the other (10 m away) with a speed of 4 ms-1 relative to the trolley in a direction opposite to the trolley’s motion and jumps out of the trolley. What is the final speed of the trolley ? How much has the trolley moved from the time the child begins to run ?
Answer:
Initial total momentum = pi = (m1 + m2) u1

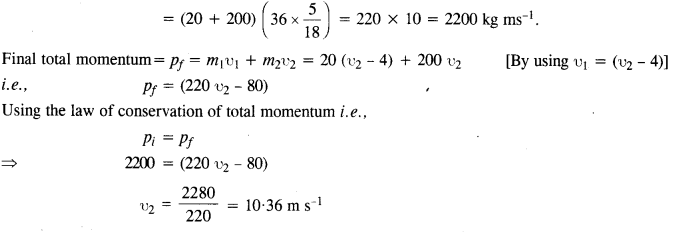
Question 29.
Which of the following potential energy curves in Fig. cannot possibly describe the elastic collision of two billiard balls ? Here r is the distance between centers of the balls.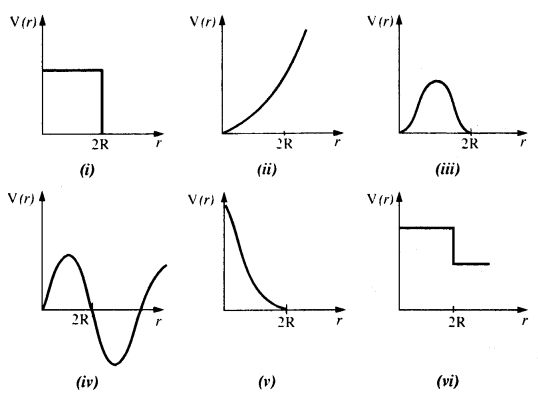

Answer:
During short time of collision, the kinetic energy converts into potential energy. Since potential energy of a system of two masses varies inversely as the distance between them i.e., as 1/r, all the potential energy curves except the one shown in fig (v) cannot describe an elastic collision.

Question 30.
Consider the decay of a free neutron at rest: n → p + e–. Show that the two-body decay of this type must necessarily give an electron of fixed energy and, therefore, cannot account for the observed continuous energy distribution in the (β-decay of a neutron or a nucleus (Fig.) [Note: The simple result of this exercise was one among the several arguments advanced by W. Pauli to predict the existence of a third particle in the decay products of (3-decay. This particle is known as neutrino. We now know that it is a particle of intrinsic spin 1/2 (like e–, p or n), but is neutral, and either massless or having an extremely small mass (compared to electron’s mass) and which interacts very weakly with matter. The correct decay process of neutron is : n —> p + e– + v]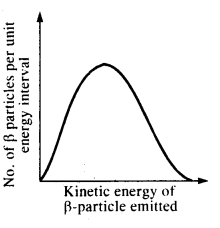

Answer:

If the decay of a neutron (inside the nucleus) into proton and electron is according to the given scheme, then the available energy in the decay must be carried by the electron coming out of the nucleus and therefore the emitted electrons should always possess a fixed value of kinetic energy. However the graph shows that the emitted electron can have any value of energy between zero and the maximum value. Therefore, the given decay mode cannot account for the observed continuous energy spectrum in the β decay.

14. Very Very Short Answer Type

Question 1.
What is the source of the kinetic energy of the falling raindrops?
Answer:
It is the gravitational potential energy that is converted into kinetic energy.

Question 2.
A spring is stretched. Is the work done by the stretching force positive or negative?
Answer:
Positive because the force and the displacement are in the same direction.

Question 3.
What is the type of collision when?
(a) Does a negatively charged body collide with a positively charged body?
Answer:
Perfectly inelastic collision.

(b) Do macroscopic bodies collide?
Answer:
Inelastic collision.

(c) Do two quartz balls collide?
Answer:
Perfectly elastic collision.

Question 4.
(a) Give two examples of potential energy other than gravitational potential energy.
Answer:
Electrostatic P.E. and elastic P.E.

(b) Give an example of a device that converts chemical energy into electrical energy.
Answer:
Daniel cell.

(c) Heat energy is converted into which type of energy in a steam engine?
Answer:
Mechanical energy.

(d) Where is the speed of the swinging pendulum maximum?
Answer:
At the bottom of the swing.

(e) A heavy stone is lowered to the ground. Is the work done by the applied force positive or negative?
Answer:
Negative work.

Question 5.
What is the work done by the centripetal force? Why?
Answer:
Zero. This is because the centripetal is always perpendicular to the displacement.

Question 6.
(a) What is the work done by the tension in the string of simple pendulum?
Answer:
zero

(b) What is the work done by a porter against the force of gravity when he is carrying a load on his hand and walking on a horizontal platform?
Answer:
zero

(c) Name the force against which the porter in part (A) is doing some work.
Answer:
Frictional force.

Question 7.
When an arrow is shot, wherefrom the arrow will acquire its K.E.?
Answer:
It is the potential energy of the bent bow which is converted into K.E.

Question 8.
When is the exchange of energy maximum during an elastic collision?
Answer:
When two colliding bodies are of the same mass, there will be a maximum exchange of energy.

Question 9.
Does the work done in raising a load onto a platform depend upon how fast it is raised?
Answer:
The work done is independent of time

Question 10.
Name the parameter which is a measure of the degree of elasticity of a body.
Answer:
Coefficient of restitution.

Question 11.
When a ball is thrown up, the magnitude of its momentum first decreases and then increases. Does this violate the conservation of momentum principle?
Answer:
No. This is because the momentum of the system (ball and air molecules) remains constant. When the momentum of the ball decreases, the momentum of air molecules in contact increases and vice-versa.

Question 12.
In a tug of war, one team is slowly giving way to the other. What work is being done and by whom?
Answer:
+ve. The winning team is performing work over the losing team.

Question 13.
A light and a heavy body have equal momentum. Which one of them has more K.E.?
Answer:
The lighter body has more K.E.

Question 14.
By using simple mechanical devices such as a lever, wedge, inclined plane, pulley, wheel, etc. we can do work even by applying small force. What makes it possible to do so?
Answer:
These mechanical devices multiply forces.

Question 15.
Two protons are brought closer. What is the effect on the potential energy of the system?
Answer:
Work is done to overcome the force of repulsion, so the potential energy of the system increases.

Question 16.
Where is the energy of a vertically projected body maximum?
Answer:
It is the same at all points. This is in accordance with the law of conservation of energy.

Question 17.
Out of a pair of identical springs of force constants, 240Nm-1 one is compressed by 10 cm and the other is stretched by 10 cm. What is the difference in the potential energies stored in the two springs?
Answer:
The difference in potential energies is zero. This is because
Ep = 12 ky2. In both cases, k and y2 are the same.

Question 18.
What should be the angle between the force and the displacement for maximum and minimum work?
Answer:
For maximum work, θ = 0° and for minimum work θ = 90°.

Question 19.
Does the P.E. of a spring decreases/increase when it is compressed or stretched? Why?
Answer:
P.E. of a spring increases in both cases. This is because work is done by us in compression as well as in stretching the spring.

Question 20.
Can a body have momentum without energy?
Answer:
No, because for momentum, it must have some velocity and hence energy.

Question 21.
What type of energy is stored in the spring of the watch?
Answer:
Potential energy.

Question 22.
Can a body have energy without momentum?
Answer:
Yes, everybody has some internal energy due to the thermal agitation of the particles of the body. But the vector sum of linear momenta of the moving particles may be zero. It may have energy due to its position (P.E.) and thus momentum is zero.

Question 23.
In which motion, momentum changes but not the K.E.?
Answer:
In uniform circular motion.

Question 24.
Is the whole of K.E. lost in any perfectly inelastic collision?
Answer:
No, only as much K.E. is lost as is necessary for the conservation of linear momentum.

Question 25.
Can the P.E. of an object be negative?
Answer:
Yes, it can be negative when the forces involved are attractive.

Question 26.
The momentum of a body is increased by 50%. What is the percentage change in its K.E.?
Answer:
When the momentum is increased by 50%, velocity increases by
i.e. velocity becomes 32 times, so K.E. becomes 94 times
i.e. 94 × 100 = 225%. Hence increase in K.E. = 225 – 100 = 125%.

Question 27.
What is the work done by Earth’s gravitational force in keeping the moon in its orbit in a complete revolution?
Answer:
Zero, because gravitational force is a conservative force.

Question 28.
A spring is cut into two equal halves. How is the spring constant of each half affected?
Answer:
The Spring constant of each half becomes twice the spring constant of the original spring.

Question 29.
What happens to the energy of our watch which we wind once a day?
Answer:
The work done in winding the watch is stored as P.E. in the spring which is converted into K.E. of the moving parts of the watch.

Question 30.
Is collision possible even without actual contact of the colliding particles? Give example.
Answer:
Yes, such collision is called collision at a distance. The collision between subatomic particles (like proton and neutrons) are examples of such collisions.

Question 31.
A cake of mud is thrown on a wall where it sticks. What happens to its initial K.E.?
Answer:
A part of the K.E. is used in deforming the cake and the remaining part is converted into heat and sound energy.

Question 32.
Nuclear fission and .fusion reactions are the examples of conversion of mass into energy. Can we say that strictly speaking, mass is converted into energy even in an exothermic chemical reaction?
Answer:
Yes, mass is converted into energy in an exothermic chemical reaction also. But the mass change in a chemical reaction is about a million times less than in a nuclear reaction.

Question 33.
What type of energy is lost in doing work against friction?
Answer:
The kinetic energy is lost in doing work against the friction.

Question 34.
Define 1 Joule.
Answer:
A joule of work is said to be done when a force of 1 N displaces a body through 1 m.

Question 35.
Define an erg.
Answer:
An erg of work is equal to work done by a force of 1 dyne of displacing a body through one centimeter.

Question 36.
Derive the relation between 1 J and 1 erg.
Answer:
We know that 1 J = 1 N × 1 m = 1 Nm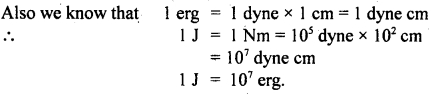

Question 37.
What is the nature of the work done by the resistive force of air on a vibrating pendulum in bringing it to rest and why?
Answer:
Negative, because the air always opposes the displacement of the pendulum bob.

Question 38.
What is the work done on a body in moving it in a circular path with a constant speed? Why?
Answer:
Zero, because it is acted upon by centripetal force in a direction perpendicular to its motion.
i.e. W = FS cos 90° = 0.

Question 39.
A truck and car are moving with the same K.E. and are brought to rest by the application of brakes that provide equal retarding force. Which one will come to rest in a shorter distance? Why?
Answer:
Both of them come to rest at the same distance as
K.E. = F.S1 = F.S2
or
FS1 cos 180 = F.S2 cos 180
or
S1 = S2.

Question 40.
A conservative force does positive work on a body. What happens to the potential energy of the body? Give an example.
Answer:
It (P.E.) decreases.
e.g. a body falling freely under gravity.

Question 41.
A man rowing a boat upstream is at rest w.r.t. the shore. Is any work being done in this case? Why?
Answer:
Yes, as there is a relative displacement between the boat and the stream.

Question 42.
Why friction is a non-conservative force?
Answer:
It is because the work done against friction along a closed path is non-zero.

Question 43.
Does the work done in raising a load onto a platform depend upon how fast it is raised?
Answer:
No, work done does not depend upon the time taken in doing it.

Question 44.
On what factors, does the work done depend?
Answer:
It depends upon the applied force and the displacement of the body.

Question 45.
How will the kinetic energy of a body change if its momentum is tripled? Why?
Answer:
K.E. becomes nine (9) times its initial value as K.E. ∝ p2.

Question 46.
Which physical quantity is conserved during both the elastic and inelastic collision?
Answer:
Linear momentum is conserved in both collisions.

Question 47.
What is the most common feature of all types of collisions?
Answer:
Linear momentum is conserved in all types of collisions.

Question 48.
Define variable force.
Answer:
It is defined as the force which either changes in magnitude or direction.

Question 49.
Give an example of variable force.
Answer:
When an object is falling towards the Earth, the gravitational force acting on it goes on changing, so it is a variable force.

Question 50.
Define an electron volt (eV).
Answer:
It is defined as the K.E. acquired by an electron when a potential difference of 1 volt is applied across it.

14 Short Answer Type

Question 1.
An airplane’s velocity is doubled,
(a) What happens to its momentum? Is the law of conservation of momentum obeyed?
Answer:
The momentum of the airplane will be doubled. Yes, the law of conservation of momentum will also be obeyed
because the increase in momentum of the airplane is simultaneously accompanied by an increase in momentum of exhaust gases.

(b) What happens to its kinetic energy? Is the law of conservation of energy obeyed?
Answer:
K.E. becomes four times. Yes, the law of conservation of energy is obeyed with the increase in K.E. coming from the chemical energy of fuel i. e. from the burning of its fuel.

Question 2.
In a thermal station, coal is used for the generation of electricity. Mention how energy changes from one form to the other. before it is transformed into electrical energy?
Answer:
When coal is burnt, heat energy is produced which converts water into steam. This steam rotates the turbine and thus heat energy is converted into mechanical energy of rotation. The generator converts this mechanical energy into electrical energy.

Question 3.
Chemical, gravitational and nuclear energies are nothing but potential energies for different types of forces in nature. Explain this statement clearly with examples.
Answer:
A system of particles has potential energy when these particles are held a certain distance apart against some force. For example, chemical energy is due to the chemical bonding between the atoms. Gravitational energy arises when the objects are held at some distance against the gravitational attraction.

Nuclear energy arises due to the nuclear force acting between the nuclear particles.

Question 4.
What went wrong at the Soviet atomic power station at Chernobyl?
Answer:
In this reactor, graphite was used as a moderator. The fuel elements were cooled by water and steam was produced from within the reactor. Both water and the steam came in contact with hot graphite. Due to this hydrogen and carbon-monoxide (CO) were released. When they came in contact with air, there was a big explosion.

Question 5.
A man can jump higher on the moon than on Earth. With the same effort can a runner improve his timing for a 100 m race on the moon as compared to that on Earth?
Answer:
Man can jump higher on the moon because the acceleration due to gravity on the moon is less than that on the Earth. But acceleration due to gravity does not affect the horizontal motion. Hence the runner can’t improve his timing on the moon for the 100 m race.

Question 6.
How many MeV are there in a 1-watt hour?
Answer:
We know that 1 watt hour = 1 JS-1 × 3600 s = 3600 J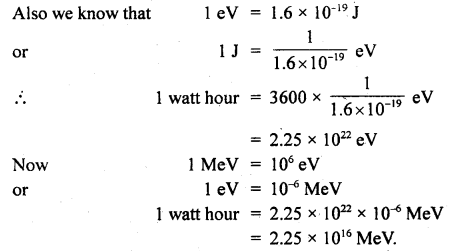

Question 7.
What is Newton’s experimental law of impact?
Answer:
The ratio of the relative speed of separation after a collision to the relative speed of approach before the collision is always constant. This constant is known as the coefficient of restitution. It is denoted by e.
∴ e = V2f−v1fu1i−u2i

where u1i and u2i, are the velocities of the bodies before collision and v2f, v1f are the velocities of the bodies after the collision.

Question 8.
Two masses one n times as heavy as the other have the same K.E. What is the ratio of their momenta?
Answer: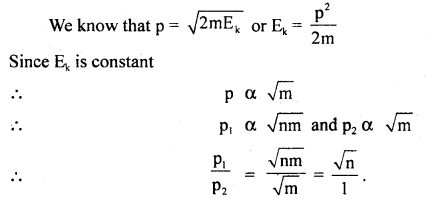

Question 9.
Two bodies A and B having masses mA and mB respectively have equal K.E. If pA and pB be their respective momenta, then prove that the ratio of momenta is equal to the square root of the ratio of respective masses. fc.
Answer:
Let vA and vB be the velocities of A and B respectively.
Since their kinetic energies are equal,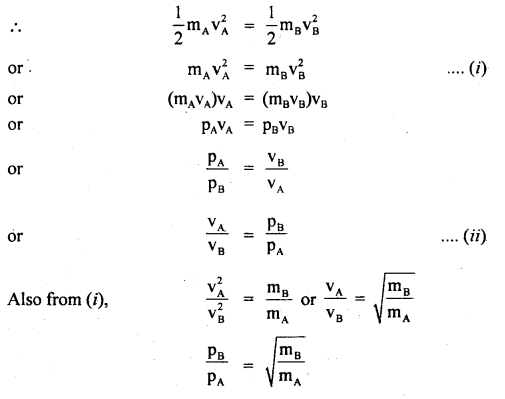


Hence Proved

Question 10.
How fast-moving neutrons can be quickly slowed down by passing through heavy water?
Answer:
Heavy water (D2O) contains deuterium atoms i.e. hydrogen nuclei. They have nearly the same mass as those of neutrons. So when neutrons strike against deuterium atoms, most of the K.E. of the former is transferred to the deuterium atoms i.e. K.E. is exchanged between them.

Question 11.
Will water at the foot of the waterfall be at a different temperature from that at the top? If yes, explain.
Answer:
Yes, when water reaches the ground, its gravitational potential energy is converted into kinetic energy which is further converted into heat energy. This raises the temperature of the water. So water at the foot of the waterfall is at a higher temperature as compared to the temperature of water at the top of the waterfall.

Question 12.
How is the kinetic energy of a particle related to the direction of motion of the particle? Can K.E. be negative?
Answer:
The kinetic energy of a particle is not related to the direction of motion of the particle. K.E. is always positive. It cannot be negative.

Question 13.
An automobile jack is employed to lift a heavyweight. The applied force is much smaller than the weight of the automobile. Can it be said that the work is done in less than the work done in? lifting the automobile directly through a height.
Answer:
No, in the case of the automobile jack, the work done is not calculated from the equation W = FS cos θ, but the work done is calculated from an equation (W = τ θ = FRθ) of rotational motion. In both cases, the same amount of work is done.

Question 14.
What would be the effect on the potential energy of the system of two electrons brought closer?
Answer:
Work has to be done to overcome the force of repulsion. This work done will be stored in the form of P.E. so, it increases the potential energy of the system.

Question 15.
Can the kinetic energy be increased without the application of an external force? If yes, give an example.
Answer:
Yes, this is possible. If work is done by the internal force, then K.E. will be increased. As an example, when a bomb explodes, the combined K.E. of all the fragments is greater than the initial K.E.

Question 16.
Mountain roads rarely go straight up the slope, but wind up gradually why?
Answer:
If roads were to go straight up, the slope (θ) would have been large, the frictional force (µmg cos θ) would be small. The wheels of the vehicle would slip. Also for going up a large slope, a greater power shall be required.

Question 17.
A truck and a car moving with the same K.E. are stopped by applying the same retarding force by means of brakes. Which one will stop at a smaller distance?
Answer:
Both will stop at the same distance which follows from the work-energy theorem.
K.E. = work done in stopping= retarding force × distance
As K.E. and force for both are equal, so the distance covered must be equal.

Question 18.
A truck and a car are moving with the same K.E. on a straight road. Their engines are simultaneously switched off. Which one will stop at a lesser distance?

Answer:
The vehicle stops when its K.E. is spent working against the force of friction between the tires and the road. This force of friction varies directly with the weight of the vehicle.

As K.E. = work done
= force of friction × distance
or
E = F × S
or
S = E/F.
Forgiven K.E., S, will be smaller where F is larger such as in the; case of a truck.

Question 19.
A man rowing a boat upstream is at rest w.r.t. the shore. Is any work being done in this case?
Answer:
No, because the man is applying the force and there is no relative motion between the boat and the shore.

Question 20.
A body is heated by giving Q an amount of heat energy. Will its mass increase or decrease or remain constant? If it increases or decreases, then by how much?
Answer:
The variation in mass depends on the nature of the body. For most solids, there is no variation in mass on heating. However, if the solid is volatile, heating will change the mass of the solid. Heating of solids, in general, bring about a change in state, and during this process, some loss of mass occurs due to evaporation.

Question 21.
A football kicked by a player leaves the ground and after traveling in the air reaches the ground and comes to stop at some other position on the ground. Identify the energy transformation in this process. Is the energy of the ball conserved?
Answer:
The kinetic energy imparted to the ball is converted into potential energy at the highest point and a small part remains kinetic. Then it is converted into kinetic energy when it hits the ground. This energy is used up in overcoming the friction against air and the ground. Due to the dissipation of energy in overcoming friction against air and ground, the kinetic energy of the ball is not conserved.

Question 22.
A child enjoys going high and high in a swing by pumping energy. Explain the large amplitude from the rest position using the work-energy idea.
Answer:
The child pumps energy to the swing at the appropriate time and place from his muscular work. In each swing friction at hinges and air, friction reduces the velocity which he compensates by providing energy to the swing at the appropriate time which partly increases the amplitude of the swing as well. So, periodic muscular work provides the energy to the swing.

Question 23.
How fast neutrons can be slowed down by heavy water? Where does the energy go?
Answer:
The fast neutrons collide with water molecules and transfer a good part of their kinetic energy to the water molecules. As a result, the kinetic energy and hence the speed of the neutrons is decreased i.e. they are slowed down. The energy received by the water molecules increases their speed and there is an increase in the thermal energy of the mass of water.

Question 24.
Show that the work done by an elastic force on a spring is stored as the potential energy of the spring.
Answer:
Consider an elastic spring that is extended or compressed. The force does not remain constant in this case. The elastic force Fel according to Newton’s Third law of motion is
Fel = – Fext
when Fext = external force applied
The Fel is always proportional to the compression or extension
i.e. Fel = – kx
∴ Fext = kx
If Fav be the average force, then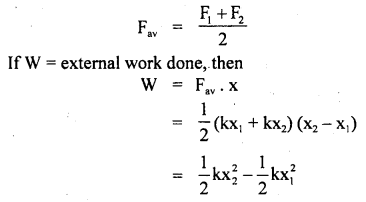

If x1 = O (choosing x1 as origin), then x2 = x
The work done by an elastic force is stored as potential energy in the spring and is given by
W = P.E. = 12 kx2.

Question 25.
What ¡s transformation of energy? Give at least five exam pies.
Answer:
The change of energy from one form to another is known as energy transformation. For example:

1. Diesel on burning produces hot gases and heat which is transformed into mechanical energy and is used to run trains and motor vehicles or pumps.
2. Electric energy is transformed into light in a tube or bulb.
3. The electric energy is changed into heat in an oven or heater.
4. Light is converted into electricity with the help of a photovoltaic cell.
5. In a microphone, sound energy is converted into electrical energy.

Question 26.
Which of the following does work: the hammer or the nail, a cricket bat or a ball? Explain.
Answer:
Hammer does work on nails. The force is applied by a hammer on the nail (object) and moves it through some distance. A bat does work on the ball and pushes. Initially, the bowler does work on the ball which init turn exerts impulse on the bat. The bat reacts with the added force of the batsman and thus, the bat does work on the ball.

Question 27.
A particle of mass m is moving in a horizontal circle of radius r under a centripetal force equal to kr2 where k is a constant. What is the total energy of the particle?
Answer:

Question 28.
What are the relations between
(a) kilowatt hour and kilocalorie?
Answer:


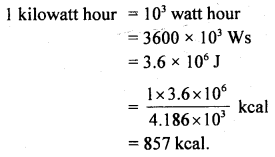
(b) metric horsepower and kilocalorie per hour?
Answer:

Question 29.
Prove that instantaneous power is given, by the dot product of force and velocity i.e. P = F.v.
Answer:
Let AW be the amount of work done in a small time interval Δt. If Pav be the average power, then

where F constant force producing a displacement S
∴ From (ii) and (iii), we get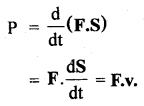

Question 30.
Define spring constant or force constant. What is its S.I. unit?
Answer:
It is defined as the extension per unit displacement produced in the spring or wire.
According to Hook’s law, the extension is always directly proportional to the tension or force applied on a spring i.e.
F ∝ x
or
F = k x
or
k = Fx

where k is the force constant
S.I unit of k is Newton metre-1 (Nm-1).

15   Long Answer Type

Question 1.
(a) State work-energy theorem or principle.
Answer:
It states that the work done on a body is equal to the change in its kinetic energy.
i.e. W = change in kinetic energy
Proof: Let m = mass of a body moving in a straight line with a constant initial velocity u.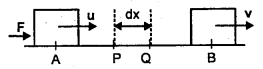

Let F = force applied on it at point A to B so that its velocity is V at B.
If dx = small displacement from P to Q
and a = acceleration produced in the body, then
F = ma

If dw be the work done from P to Q, then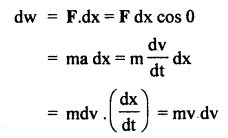

If W = total work done from A to B, then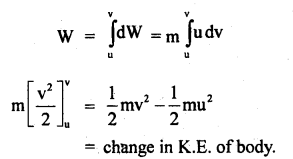

(b) State and prove the law of conservation of energy.
Answer:
It states that energy can neither be created nor can be destroyed but it can be changed from one form of energy into another i.e. total energy = constant.

Proof: Let a body of mass m be lying at rest at point A at a height h above the ground. Let it be allowed to fall freely and reaches a point B after falling through a distance x and it finally hits the ground at point C. Let v and V be its velocities at points B and C respectively.
∴ AB = x and BC = h – x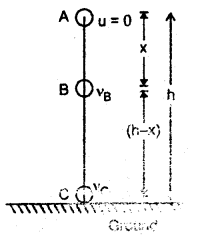

At point A: u = 0
∴ K.E. = 0
P.E. = mgh

If E be the total energy of the body, then
E = K.E. + P.E. = 0 + mgh
or
E = mgh …. (i)

At point B: using the relation,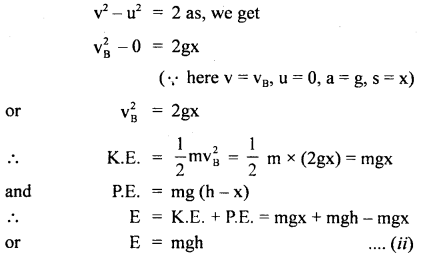

At point C: Here, v = vc, a = g, s = h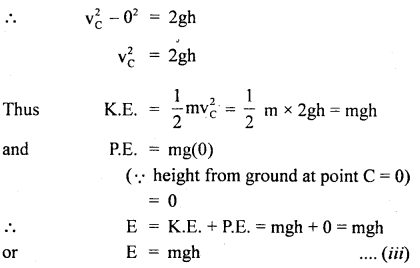

Thus, from (i), (ii), and (iii), it is clear that total energy at points A, B, and C is the same. It is purely P.E. at A and purely K.E. at point C.

16

Numerical Problems:

Question 1.
An engine draws a train up an incline of 1 in 100 at the rate of 36 km h-1. If the resistance due to friction is 5 kg wt per ton, calculate the power of the engine. Mass of train and engine is 100

Answer:
Here, m = 100 metric ton = 100 × 1000 kg
Total force of friction,
f1 = 100 × 5 = 500 kg wt
= 500 × 9.8 N = 4900 N
sin θ = 1100

Let f2 = Downward force on the train
= component of its weight acting in downward direction parallel to the inclined plane = mg sin θ
= 100 × 1000 × 9.8 × 1100 = 9800 N

If F be the total force against which engine has to work, then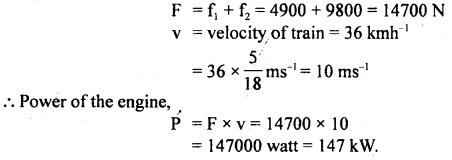

Question 2.
Calculate the work done and power of an engine that can maintain a speed of SO ms-1 for a train of mass 3 × 106 kg on a rough level track for 5 km. The coefficient of friction is 0.05. Given g = 10 ms-2.
Answer:
Here,

Question 3.
A 10 kg block slides without acceleration down a rough inclined plane making an angle of 20° with the horizontal. Calculate the work done over a distance of 1.2 m when the inclination of the plane is increased to 30°.
Answer:
Here, angle of sliding = 20°
μ = coefficient of friction
= tan 20° = 0.3647
S = 1.2 m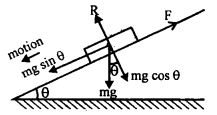

m = mass of block = 10 kg.

Let a = acceleration when the inclination is increased to 30° and F be the value of limiting friction then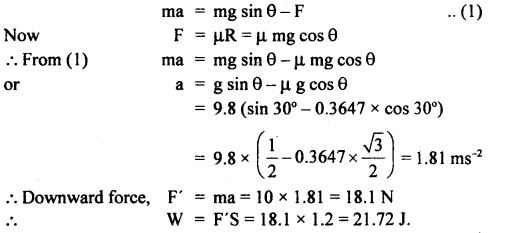

Question 4.
A bullet of mass 0.03 kg moving with a speed of 400 ms-1 penetrates 12 cms into a fixed block of wood. Calculate the average force exerted by the wood on the bullet.
Answer:
Here,
mass of bullet, m = 0.03 kg
initial K.E. = 12mv2 = 12 × 0.03 × (400)2 = 2400 J
Final K.E. = 12mv2 = 0

∴ ΔK = Loss in kinetic energy = 2400 J
Let F = average force applied by block on bullet
S = 0.12 m

∴According to work energy principle
W = ΔK
or
FS = ΔK
or
F × 0.12 = 2400
or
F = 2 × 104 N

Question 5.
A boy of mass 50 kg sits in a swing suspended, by a rope 5 m long. A person pulls the swing to one side so that the rope makes an angle of 30° with the vertical. What is the gain in gravitational P.E. of the boy?
Answer:
Here, θ = 30°
OA = OB = 5 m …. (i)
m = 50 kg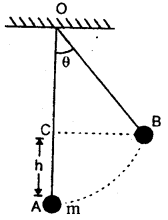

Vertical height through which boy at B rises up is given by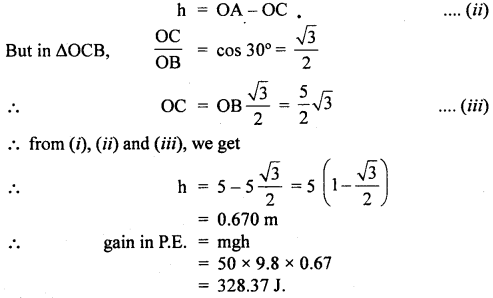

Question 6.
(a) bullet of mass 20 g moving with a velocity of 500 ms-1 strikes a tree and goes out from the other end. with a velocity of 400 ms-1. Calculate the work done in passing through the tree.
Answer:
Here m = 0.02 kg
u = 500 ms-1
v = 400 ms-1
w = ?
from work energy theorem, work done loss in K.E.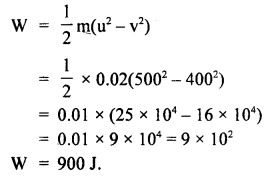

(b) A bullet of mass 0.01 kg is fired horizontally into a 4 kg wooden block at rest on a horizontal surface. The coefficient of kinetic friction between the block and the surface is 0.25. The bullet remains embedded in the block and the combination moves 20 m before coming to rest. With what speed did the bullet strike the block?
Answer:
Here S = 20 m
μ = 0.25
M = mass of block = 4 kg
m = mass of bullet = 0.01 kg

∴ R = normal reaction = Mg = 4 × 9.8
F = μR = 0.25 × 4 × 9.8 = 9.8 N
v = 0
u = ?
or
loss in KE. = work done by the force of friction against the block.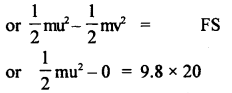

Question 7.
A stone of mass 5 kg falls from the top of a cliff 30 m high and buries itself one meter deep into the sand. Find the average resistance offered and time taken to penetrate into the sand.
Answer:
Here, m = 5 kg
h = 30 m
S = 1 m
∴ P.E. of stone = mgh = 5 × 9.8 × 30 = 1470 J

Let F = average force of resistance offered by the sand and F’ = net upward force.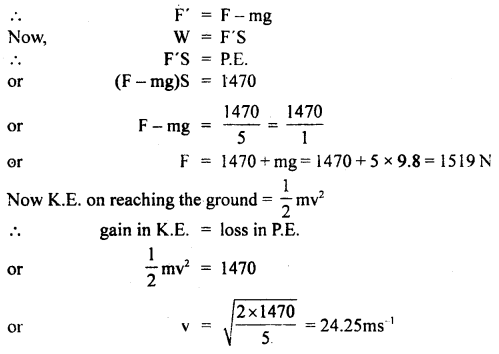

Now momentum of stone before penetration
mu = mv = 5 × 24.25 (∵ here u = v)

Final momentum of stone when it becomes stationary (i.e. v’ = 0)
= mv’ = m(0) = 0
∴ Ft = – mv’ + mu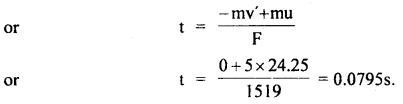

Question 8.
An automobile moving at a speed of 72 km h-1 reaches the foot of a smooth incline when the engine is switched off. How much distance does the automobile go up the incline before coming to rest? Take angle of incline 30°, g = 9.8 ms-2.
Answer:
Here, θ = 30°
Initial velocity of the automobile at point A when it is switched off = 72 kmh-1
= 72 × 518 = 20 ms-1

Let m = mass of automobile.
Initial K.E. of the automobile at A = 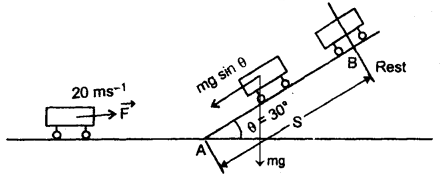12 m(20)2 = 200 m

F = mg sin θ = force opposing the motion of the automobile
= m × 9.8 sin 30° = (4.9m)N

Let it stop at B after travelling AB = S
∴ Final K.E. = 0
∴ change in K.E. = 200m – 0 = 200m J
∴ W = work done by the automobile
= FS = (mg sin θ) × S = 4.9 m × S

∴ According to work-energy theorem,
W = change in K.E.
or
4.9m S = 200m
or
S = 2004.9 = 40.8m

Question 9.
A pump-set is used to lift water to a reservoir of 6000 liters capacity over an average height of 20m. If it takes 1 hour to All the reservoir completely, calculate the work done and the power supplied to the set if its efficiency is 60%, g = 9.8 ms-2.
Answer:
Mass of 1 litre of water = 1 kg .
∴ m = 6000 kg
h = 20 m

∴ W = work done = P.E. = mgh
= 6000 × 9.8 × 20= 11.76 × 10s J
t = 1 h = 3600 s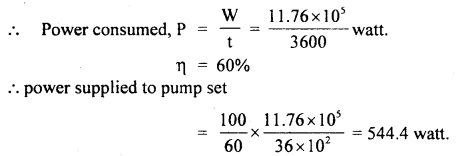

Question 10.
A wooden ball is dropped from a height of 2 m. What is the height up to which the ball will rebound if the coefficient of restitution is 0.5?
Answer:
Here, e =0.5
Let the ball fall from a height h1 from point A and rebound to B at a height of h2.
∴ h1 = 2 m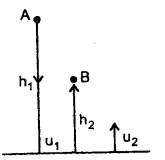

∴ If u1 be the velocity on reaching the ground = velocity of approach and u2 = Velocity on leaving the ground = velocity of separation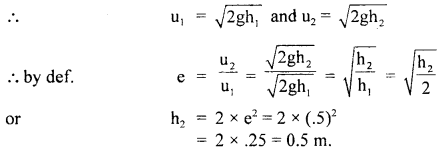

Question 11.
What percentage of K.E. of a moving particle is transferred to the stationary particle of
(a) 9 times it’s mass
Answer:
Let m1 = mass of moving particle = m
and m2 = mass of stationary particle = 9 m
and their velocities are u1 and u2 = 0 (given)
v2 = velocity of the stationary particle after the collision.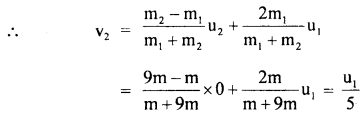

So, % of K.E. transferred to the stationary particle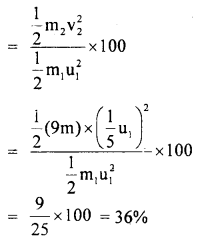

(b) equal mass,
Answer: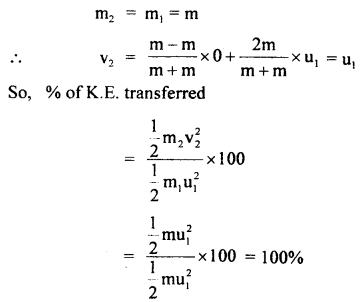

(c) 19 th of its mass.
Answer: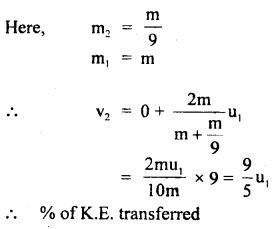

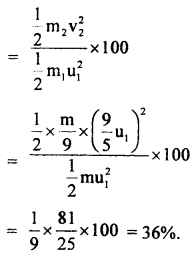
Question 12.
Calculate the work done in raising a stone of mass 6 kg of specific gravity 2 immersed in water from a depth of 4 m to 1 m below the surface of the water. Take g = 10 ms-2.
Answer:
Here, m = 6 kg
∴ weight of stone = 6 × 10 = 60 N
specific gravity of stone = 2
∴ d = density of stone
= 2 × lg cm-3
= 2g cm-3.

∴ volume of stone = md=6×1000 g2gcm−3 = 3000 cm3
= 3000 × 10-6 m3
= 3 × 10-3 m3
= volume of displaced water.

Weight of water displaced or upward thrust on the stone
= volume × density of water × g
= 3 × 10-3 × 1000 × 10 = 30 N

∴ The net force acting on the stone = weight of stone – upward thrust on the stone
or F = 60 – 30 = 30 N
Distance through which stone is raised = (4 – 1 )m = 3m
∴ work done, W = FS = 30 × 3 = 90 J.

Question 13.
An antenna radiates energy for 24 hours at the rate of 1 kW. Calculate the equivalent mass for radiated energy.
Answer: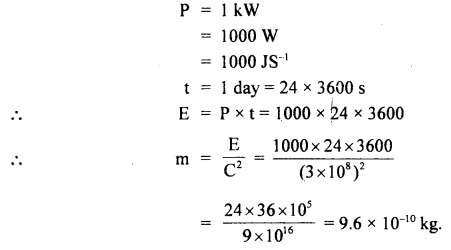

Question 14.
A particle moves from position r1 = 3î + 2ĵ – 6k̂ to position r2 = 14î + 13ĵ – 9k̂ under the action of a force (4î + ĵ + 3k̂)N. Calculate the work done.
Answer:
Here, F = (4î + ĵ + 3k̂)N
Displacement of the particle,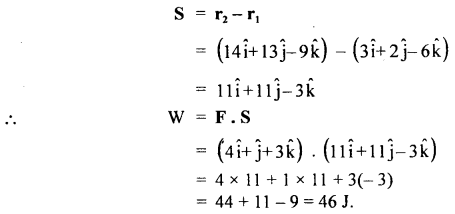

Question 15.
The displacement x of a particle moving in one dimension under the action of a constant force is related to the time by the equation t = x−−√ + 3.
where x is in meters and t is in seconds.
Find (i) the displacement of the particle when its velocity is zero and
(ii) work is done by force in the first six seconds.
Answer: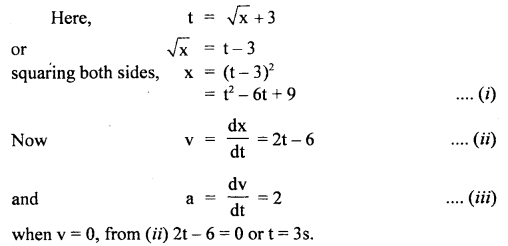

Question 16.
A 1 kg mass on a floor is connected to a 2 kg mass by a string passing over a pulley as shown in the figure. Obtain the speed of the masses (after they are released) when the 2 kg mass just touches the floor. Show that the gain in kinetic energy of the system equals the loss in its potential energy. The 2 kg mass is initially at a height 3 m above the ground.
Answer:
Here, m2 = 1kg
m1 = 2kg
u = 0
h = 3m
The system is shown in the figure. According to Newton’s Second law of motion, the equation of motion for 2 kg mass is
mg – T = ma
or
2 × 9.8 – T = 2a …(i)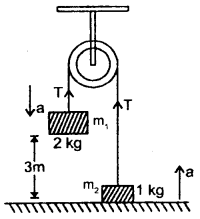


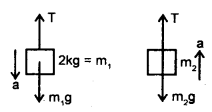
(Free body diagrams of m1 and m2)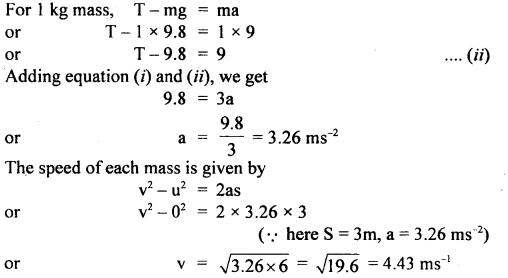

Since both the masses are initially at rest, therefore initial K.E. of the system = 0
Final K.E. of the system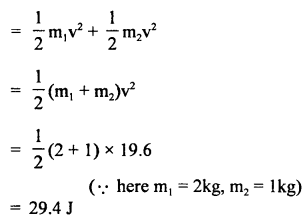

∴ Gain in K.E. = 29.4 – 0 = 29.4 J
Initially P.E. of the system = m1gh1 + m2gh2
= 2 × 9.8 × 3 + 1 × 9.8 × 0
= 58.8 J ( ∵ here h2 = 0)

Finally, the 2 kg reaches the floor and mass 1 kg is at a height of 3m.
∴ Final P.E. of the system = m1gh1 + m2gh2
= m1g × 0 + 1 × 9.8 × 3
= 29.4 J

∴ Loss of P.E. = 58.8 – 29.4
= 29.4 J
Thus Gain in K.E. = Loss of P.E. = 29.4 J.

Question 17.
A homogeneous and inextensible chain of length 2 m and mass 100 g lies on a smooth table, A small portion of the chain of length 0.5 m hangs from the table. Initially, the part of the chain lying on the table held and then released. Calculate the velocity with which the chain leaves the table, g = 10 ms’2.
Answer:
Mass of chain, M = 100 g = 0.1 kg
length of chain, l = 2 m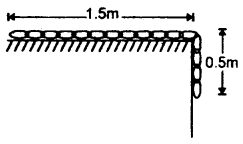

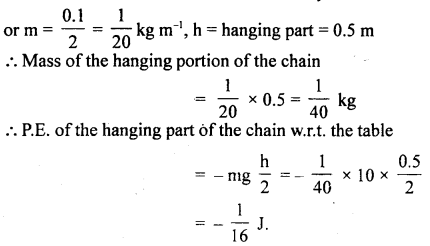
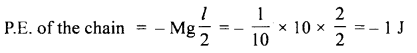
∴ Mass per unit length of the chain, m = Ml


Let v = velocity of the chain when it leaves the table.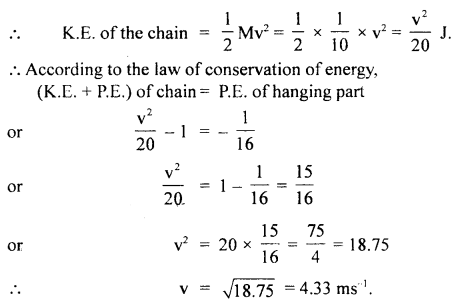

Question 18.
The K.E. of a body increases by 300%. How much linear momentum of the body will increase?
Answer: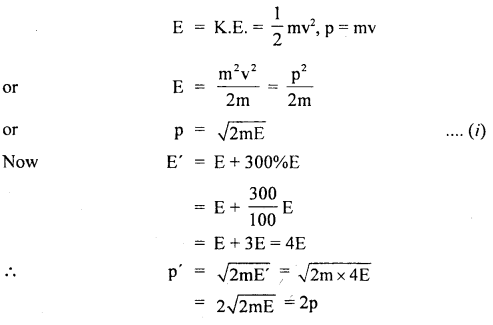

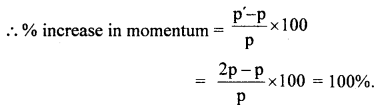
Question 19.
A ball falls under gravity from a height of 10m with an initial downward velocity of u. It collides with the ground, loses 50% of its energy in the collision, and then rises back to the same height. Find the initial velocity u.
Answer:
Here, u = initial velocity of the ball
h = its height

Let M = mass of the ball
∴ The total initial energy of the ball at height h,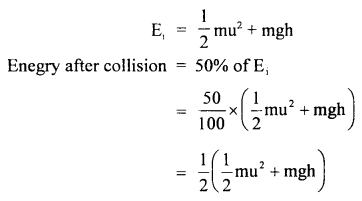

The ball rises to height h due to this energy.
∴ P.E. of ball = mgh
∴ According to the law of conservation of energy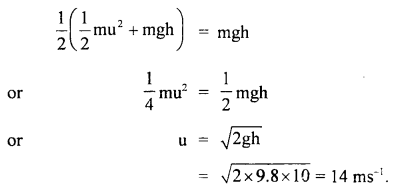

Question 20.
The heart of a man pumps 4-liter blood per minute at a pressure of 130 mm of mercury. If the density of mercury is 13.6 gm cm3, then calculate the power of the heart.
Answer:
Here, the height of the mercury column,

Question 21.
A body is allowed to fall from a height of 100 m. Find the increase in temperature of the body on reaching the ground if the whole of heat produced remains in the body. Given that the specific heat of the body = 0.2, J = 4.2 J cal-1.
Answer:
Loss in P.E. of the body in falling through 100 m = m × 9.8 × 100 J = 980 m4.2 (∵ P.E = mgh)

This loss is transformed into the heat state of the body = ms θ
where θ = rise in temperature.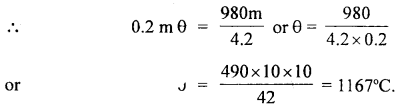

Question 22.
A truck of mass 2000 kg has a velocity of 8 ms-1 when it starts from a point to descend a slope 200 m long. The vertical height of the slope is 18 m and the truck arrives at the bottom with a velocity of 20 ms-1. Calculate the resistance offered.
Take g = 10 ms-2.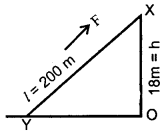

Answer:
Here, l = XY = length of slope.
= 200 m
OX = h = 18 m
Let u and v be the velocities of the .truck at points X and Y respectively.

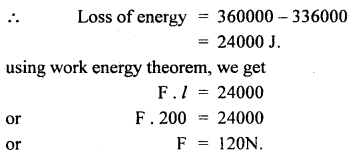
Question 23.
A body of mass m slowly hauled up the hill by a force F which at each point was directed along a tangent to the trajectory. Find the work performed by this force if the height of the hill is h, the length of its base is l, and the coefficient of friction is μ.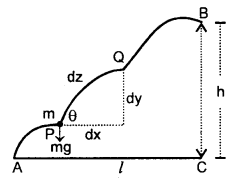

Answer:
Let PQ be the plane patch of the hill
dz = its length inclined at an angle θ with the horizontal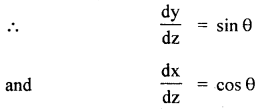

Force required to move the mass from P to Q
= mg sin θ + μmg cos θ

∴ Work done from P to Q = mg (sin θ + μcos θ).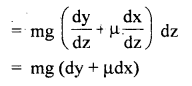

∴ W = total work done in moving the mass m from A to B is given by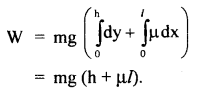

Question 24.
A chain of mass m and length l lying on a rough table starts sliding off the table all by itself till the hanging part equals n. Calculate the total work performed by the friction forces acting on the chain by the moment it slides off the table completely.
Answer:
Weight of suspended chain = n mg
weight of the part of the chain on the table = (1 – n) mg

Let μ = coefficient of friction of tabletop.
For sliding motion of the chain on the tabletop under the weight of’ the hanging chain,
μ(l – n) mg = n mg
or
μ = n1–n …(i)

The initial force of friction when the chain is pulled on the tabletop
= μ(1 – n)mg

Final force, when all the chain has been pulled = 0
mean friction = μ(1−n)mg2

Distance for which the chain is pulled = – (1 – n)l
∴ W = mean force × distance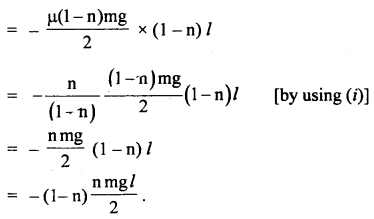

Question 25.
A flexible chain of length l and mass m is slowly pulled up at a constant speed over the edge of a table by a force F(x) parallel to the edge of the tabletop. Calculate the work done by F(x).
Answer:
Here the force required to pull the chain over the table varies with distance.
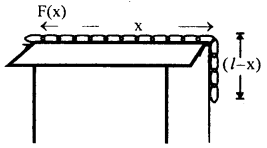
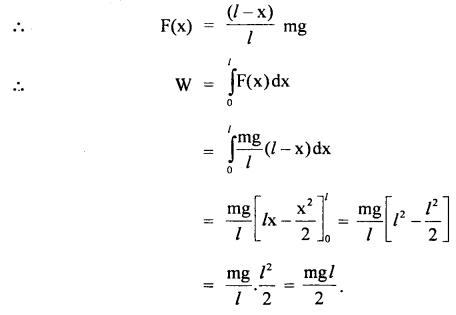
It is equal to the weight of the fraction of the chain (l−x)lstill hanging over the edge.

17

Value-Based Type:

Question 1.
Rajesh and Rakesh are two friends who participated in a quiz contest. The teacher asked Ramesh to lift a 20 kg weight vertically upwards to a height of 10 m and Rakesh asked to pull 20 kg of weight by a rope over a pulley from a depth of 10 m from a well. There was a prize for one who will do more work. Rajesh claimed that he has done more work than Rakesh because he has not used any kind of lever. The teacher told Rajesh that he has done zero work but Rakesh has done the work. Hence, the prizes were given to Rakesh
(i) Why the teacher told that Rajesh did not do any work? justify your answer.
Answer:

1. The teacher wanted to check the knowledge of physics and awareness in a playful manner.
   He used the demonstration method to create interest.
2. We know that:
   W = F d cos θ
   In the case of Rajesh:
   θ = 90° and cos 90°=o
   ∴ work done(w) =Fd × o = o
   Hence, no work was done.

Question 2.
Shikha is doing her Engineering from IIT Delhi. Her mother was also an Engineer who wanted to check the knowledge of her daughter. She asked a question as to under. “If we assume that the moon orbits around the earth is perfectly circular then the earth’s gravitational force does no work. Is it correct?”
She explained that the moon’s displacement is tangential Whereas the earth’s force is inwards and θ = π2
So, W = F.d. cos π2 = o
(i) Which values are displayed by Shikha?
Answer:
Values displayed are:
Explanatory, intelligent, cooperative.

(ii) Why her mother asked such a question?
Answer:
Her mother wanted to test the knowledge and presence of mind of her daughter to ask such type of tricky questions.

Question 3.
Suraj went to Big Bazaar to purchase certain goods. There he has noticed an old lady struggling with her shopping. Immediately he showed her the lift and explained to her how it carries the load from one floor to the next. Even then the old lady was not convinced. Then Suraj took her in the lift and showed her how to operate it..

That old lady was very happy.
(a) What values does Suraj possess?
Answer:
Suraj is sympathetic and also has the attitude of helping others. He has patience.

(b) An elevator can carry a maximum load if 1800 kg is moving up with a constant speed of 2 m/s, The frictional force opposing the motion is 4000 N. Determine the minimum power delivered by the motor to the elevator in watts as well as in horsepower.
Answer:
The downward force on the elevator is
F = mg + Ff = (1800 × 10) + 4000 = 22000 N

The motor must supply enough power to balance this force.
Hence P = F.V = 22000 × 2 = 44000 = 59 hp