Showing posts with label Phys XI 05. Show all posts
Showing posts with label Phys XI 05. Show all posts

Class 11: Physics Chapter 5: Laws of Motion

 Laws of Motion 



LAWS OF MOTION

ARISTOTLE’S FALLACY

  • Aristotelian law of motion states: An external force is required to keep a body in motion.
  • Galileo disproved this by experiments using inclined planes.

GALILEO’S EXPERIMENTS

Using a single inclined plane

  • Galileo studied the motion of objects on an inclined plane.
  • Objects moving
    1. down an inclined plane, get accelerated,
    2. up an inclined plane, retarded,
    3. on a horizontal plane, is an intermediate situation.







  • Galileo concluded that an object moving on a frictionless horizontal plane should move with constant velocity.

Using Double inclined plane

 


  • A ball released from rest on one of the planes rolls down and climbs up the other.
  • When friction is absent, the final height of the ball is the same as its initial height.
  • If the slope of the second plane is decreased and the experiment repeated, the ball will still reach the same height, but it will travel a longer distance.
  • When the slope of the second plane is zero (i.e., is a horizontal) the ball travels an infinite distance.
  • If there were no friction, the ball would continue to move with a constant velocity on the horizontal plane.
  • Thus, according to Galileo, the state of rest and the state of uniform linear motion (motion with constant velocity) are equivalent.
  • If the net external force is zero, a body at rest continues to remain at rest and a body in motion continues to move with a uniform velocity.

NEWTON’S LAWS OF MOTION

  • Starting from Galileo’s ideas, Newton formed three laws of motion.

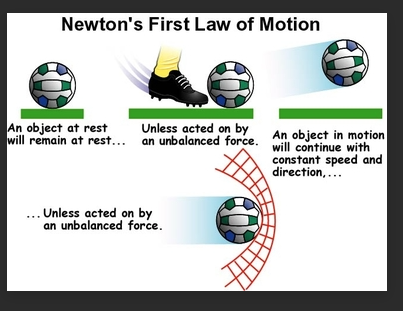
NEWTON’S FIRST LAW OF MOTION – THE LAW OF INERTIA

  • Everybody continues to be in its state of rest or of uniform motion in a straight line unless and until compelled by some external force to act otherwise.

INERTIA

  • The inability of a body to change its state of rest or uniform motion along a straight line.
  • Inertia means resistance to change.

Inertia of rest (static inertia)

  • The property of an object by virtue of which it remains in its state of rest.
  • Examples:
    1. a person standing in a bus tends to fall backward when the bus starts suddenly
    2. Fruits fall down due to inertia of rest when the branches of a tree are shaken
    3. Dust particles on a carpet fall if we beat the carpet with a stick
    4. With a quick pull, a table cloth can be removed from a dining table without disturbing dishes on it due to the Inertia of rest.

Inertia of motion (kinetic inertia)

  • The property by which it remains in state of motion
  1. A person in running bus , falls forward the bus when stops suddenly.
  2. Athlete taking a short run before a jump.

Forces on a book at rest on a horizontal surface



The two forces are

i) the force due to gravity (i.e., its weight W) acting downward

ii) the upward force on the book by the table, the normal force R.

  • Since the book is rest the net force on the book must be zero.

Forces on a car




  • When the car is stationary, there is no net force acting on it.
  • During pick-up, it accelerates. It is the frictional force that accelerates the car as a whole.
  • When the car moves with constant velocity, there is no net external force.
  • Friction on the front wheels opposes the spinning, so friction must point in the forward direction.

MOMENTUM ( P )

• Momentum is the product of its mass and velocity

The three rectangular components of Force can be represented as follows.




    • PROBLEM

    • A bullet of mass 0.04 kg moving with a speed of 90 m s-1 enters a heavy wooden block and is stopped after a distance of 60 cm. What is the average resistive force exerted by the block on the bullet?

    Solution

    • Given m=0.04kg, v0 = 90 m/s , x= 0.6m, v=0
    • The acceleration of the bullet is given by

    Impulse

    • The product of force and time.

     = Change in Momentum

    • Unit of impulse is newton-second (Ns).

    Impulsive force

    • A large force acting for a short time to produce a finite change in momentum.
    • Examples are force when a ball hits on a wall, force exerted by a bat on a ball, force on a nail by a hammer etc.

    PROBLEM

    • A batsman hits back a ball straight in the direction of the bowler without changing its initial speed of 12 m s–1. If the mass of the ball is 0.15 kg, determine the impulse imparted to the ball. (Assume linear motion of the ball

    Solution

    Impulse = Change in momentum

    NEWTON’S THIRD LAW OF MOTION

    • To every action, there is always an equal and opposite reaction.
    • Forces always occur in pairs. Force on a body A by B is equal and opposite to the force on the body B by A.
    • Action and reaction force occurs simultaneously.
    • Action and reaction forces act on different bodies, not on the same body – they do not cancel each other.

    Examples

    • When a man walks on earth he exerts a force in the backward direction- Action The earth exerts an equal reaction on man in the forward direction. As a result, he moves in forward direction.
    • When a bird flies it exerts a force on the air by its wings.

    The air exerts a reaction force on the wings in the opposite direction. As a result, the bird flies.

    • When a bullet is fired from a gun , the force exerted on the bullet is action. The bullet exerts a reaction force on the gun in the opposite direction- recoil of gun
    • In a rocket the burnt gas at a very high-pressure escapes through the nozzle with a tremendous force.

    This escaping gas exerts a reaction force on the rocket in the opposite direction. Thus, rocket moves forward

    PROBLEM

    • Two identical billiard balls strike a rigid wall with the same speed but at different angles, and get reflected without any change in speed as shown in fig. What is

    1. The direction of the force on the wall due to each ball?
    2. the ratio of the magnitudes of impulses imparted to the balls by the wall?

    Solution

    i) To find the direction of force, impulse (change in momentum) of the ball is

    calculated.

    Case (a)

    • Therefore x – component of impulse = – 2mu
    • y – component of impulse = 0
    • Impulse and force are in the same direction
    • Thus, the force on the ball due to the wall is normal to the wall, along the negative X-direction.
    • From Newton’s Third law, the force on the wall due to the ball is normal to the wall, along the positive x-direction.
    Case (b)

    • Thus

    • Therefore, the force on the wall due to the ball is normal to the wall, along the positive X-direction.

    ii) The ratio of the magnitudes of the impulses imparted to the balls is

    THE LAW OF CONSERVATION OF MOMENTUM

    • The total momentum of an isolated system ( a system with no external force ) of interacting particles is conserved.
    • From Newton’s second law  

    • Therefore, when F=0, initial momentum = final momentum.

     

    Applications of conservation of momentum:

     Recoil of a gun

    • Velocity of a bullet- muzzle velocity
    • Movement of gun backward, when a bullet is fired- recoil of gun
    • According to conservation of momentum momentum before firing = momentum after firing.
    • Thus

    Where m- mass of bullet, u- velocity of bullet, M- mass of gun, V- recoil velocity of gun

    • Therefore

    • The negative sign shows that velocity of gun is opposite to that of bullet
    • Recoil velocity is very small (since M > m)

     

    Rocket propulsion

    • When a rocket is fired, fuel is burnt in the combustion chamber.
    • The hot gas at very high-pressure escapes through the nozzle with a very high velocity
    • The escaping gas has a very high momentum
    • In order to conserve momentum, the rocket moves in the forward direction.

     

    EQUILIBRIUM OF A PARTICLE

    • Equilibrium of a particle in mechanics refers to the situation when the net external force on the particle is zero.
    • The forces acting at a point are called concurrent forces
    • If two forces F1 and F2, act on a particle, equilibrium requires

    • Equilibrium under three concurrent forces F1, F2 and F3 requires that

    COMMON FORCES IN MECHANICS

    i) Gravitational force –

    • Every object on the earth experiences the force of gravity due to the earth.

    ii) Contact forces

    • A contact force on an object arises due to contact with some other object: solid or fluid.
    • When bodies are in contact there are mutual contact forces (for each pair of bodies) satisfying the third law.
    • The component of contact force normal to the surfaces in contact is called normal reaction.
    • The component parallel to the surfaces in contact is called friction.

    iii) Force due to spring

    • When a spring is compressed or extended by an external force, a restoring force is generated.
    • This force is usually proportional to the compression or elongation (for small displacements).
    • The spring force F is written as F = – k x where x is the displacement and k is the force constant.
    • The negative sign denotes that the force is opposite to the displacement from the unstretched state.

    iv) Tension in a string ( T )

    • The restoring force in a string is called tension.
    • The direction is always away from the body

    The different contact forces of mechanics mentioned above fundamentally arise from electrical forces.

    MOTION OF CONNECTED BODIES

    Body moving on a horizontal frictionless table

    Motion in a frictionless pulley

    • And

    Motion in a lift

    a) Lift at rest or moving with constant velocity upward or downward

    • Here acceleration a=0
    • The net force is

    • Thus apparent weight = Actual weight

    b) Lift moves up with acceleration a

    • The net force

    • Apparent weight > Actual weight

    c) Lift moves down with acceleration a

    • The net force

    • Apparent weight < Actual weight

    d) Lift falls down freely

    FRICTION

    • Friction is the force which opposes the relative motion between two surfaces in contact.
    • It acts tangential to the surface of contact.
    • Arises due to
    1. adhesive force between surfaces
    2. irregularities of plane surface
    • There are two types

    i) Static friction

    ii) Kinetic friction

    Read more »
    Subhas C Chakra at No comments:
    Labels:
    Subscribe to: Posts (Atom)

    Physics class 12 chapter 15 : Communication Systems

      Chapter -15 COMMUNICATION SYSTEMS COMMUNICATION SYSTEM The terms communication signifies transmission reception processing of information ...

    Article of the Year