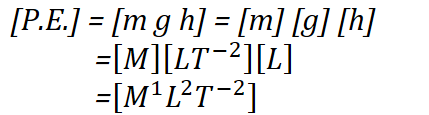Class 11- Chapter 2- : Units And Measurements

 In this Chapter we have to discuss the following concepts:

• Physical quantity
• Types of Physical quantities
• Unit
• System of Units
• Supplementary Units
• Measurement of Length
• Measurement of Short lengths
• Measurement of Large lengths
• Parallax method
• Special Units for short and large lengths
• Measurement of Mass
• Measurement of Time
• Accuracy and Precision in Measurements
• Errors in Measurements
• Types of Errors
• Systematic Errors
• Random Errors
• Least Count Errors
• Estimation of Errors
• Absolute Error
• Mean Absolute Error
• Relative Error
• Percentage Error
• Combination of Errors
• Errors in a Sum or Difference
• Errors in a Product or Quotient
• Significant Figures
• Rules for determining Significant Figures
• Scientific notations
• Order of Magnitude of a Physical Quantity
• Approximation or rounding off the uncertain digits
• Dimensions of Physical quantities
• Dimensional formula
• Dimensional Equation
• Principle of Homogeneity
• Dimensional Analysis
• The CCC of Dimensional Analysis
• Correction
• Conversion
• Correlation

Physical quantity: 

• Any quantity that can be measured is a physical quantity.
• A physical quantity can be classified in to two types:-

1. Fundamental quantity 
2. Derived quantity

• Fundamental quantity: Quantities that can not be expressed in terms of other quantities are known as fundamental quantities.
• Example:-Mass, Length, Time, Electric current  etc.

• Derived quantity: Quantities which are derived from fundamental quantities are known as derived quantities. 
• Example:- force, momentum, velocity, density, area, volume , etc.

Unit :

In order that it would be called a unit, it must possess these three characteristics. 

• Universal acceptance: Basic, internationally accepted reference standard used for measurement is called unit.

• User-friendliness: The size of the unit should be comfortable for the user.

• Perennial nature : The unit should remain constant over a vast range of time.

Other facts about Units:

• The units for the fundamental or base quantities are called fundamental or base units.
• The units of all other physical quantities can be expressed as combinations of the base units.
• Units obtained for the derived quantities are called derived units.

Systems of Units :

• A complete set of the fundamental or base units and derived units, is known as the system of units.
• In CGS system the base units for length, mass and time are centimetre , gram and second respectively.
• In FPS system the base units for length, mass and time were foot, pound and second respectively.
• In MKS system the base units for length, mass and time were metre, kilogram and second respectively.
• In S.I. System of Units,  the base units for length, mass , time, electric current, thermodynamic temperature, luminousity and amount of substance  are metre, kilogram , second, Ampere, Kelvin, Candela and Mole  respectively.
• The two supplementary units are Radian and Steradian for plane angle and solid angle respectively.

THE INTERNATIONAL SYSTEM OF UNITS

• SI system is at present the internationally accepted system of units .
• In SI, there are seven base units and two supplementary units.

Serial No.	SI Units Fundamental quantity
		Name	Symbol
1	Length	metre	m
2	Mass	kilogram	kg
3	Time	second	s
4	Electric Current	ampere	A
5	Temperature	kelvin	K
6	Amount of substance	mole	mol
7	Luminous intensity	candela	cd

 

Serial No.	S.I. Units   Supplementary quantity	Name	Symbol
1	Plane angle	radian	rad
2	Solid angle	steradian	sr

 

Plane angle

The plane angle ,  dθ = ds/r, where ds represents the length of arc linked with the small angle dθ.

Solid angle

 

The solid angle , dΩ = dA/r2 or dS/r2         

 where dA or dS  represents the area of surface linked with the small solid angle ,

 dΩ   

Prefixes used with SI units

Prefix	Symbol	Meaning
Tera –	T	1012
Giga-	G	109
Mega-	M	106
Kilo-	K	103
Deci-	d	10-1
Centi –	c	10-2
Milli-	m	10-3
Micro	µ	10-6
Nano	n	10-9
Pico	p	10-12

MEASUREMENT OF LENGTH:

• A Metre Scale is used for lengths from 10-3 m to 102m (1 mm to 100 m).
• A Vernier Calipers is used for lengths to an accuracy of 10-4m.
• A Screw Gauge or a Spherometer can be used to measure lengths as less as to 10-5m.

Measurement of large distances

Parallax method

Parallax method to find distance of a star, far away :

• This method is used  to measure distances for   objects, large distances away.
• The apparent shift in the position of an object when viewed from two different positions is known as parallax.
• The distance between the two points of observation is called the basis.

• Step-1: The star is viewed from two different positions from earth and the angle is measured.
• Step-2: By using the equation , Angle = Arc/Radius , we get

θ = b /D

• Step-3 : Hence, D = b/θ

Parallax method to find diameter of a star

• Step-1: Two diametrically opposite points on star are viewed from the same location on the earth and α is measured.
• Step-2: If D=2R is the diameter of the planet and d is the distance  of the star

α = D/d =2R/d

• Step-3: Hence,  D =α ×d , where d= distance of the star.

PROBLEM -1

• Calculate the angle of (a) 10 (degree) , (b) 1′ (minute of arc or arcmin) and (c) 1″ (second of arc or arc second) in radians. Use 3600=2π rad, 10=60′ and1′ = 60 ″

Solution

PROBLEM -2

• The moon is observed from two diametrically opposite points A and B on Earth. The angle θ subtended at the moon by the two directions of observation is 1o 54′ . Given the diameter of the Earth to be about 1.276 × 107 m, compute the distance of the moon from the Earth.

Solution

 PROBLEM -3

• The Sun’s angular diameter is measured to be 1920′′. The distance D of the Sun from the Earth is 1.496 × 1011 m. What is the diameter of the Sun ?

Solution

Estimation of Very Small Distances :

•  special methods like thin film techniques are used, to measure the size of a molecule.
• Electron microscopes can  resolve atoms or molecule in a material.
• In  tunneling microscopy   developed recently, the limit of resolution is better than an angstrom.

SPECIAL UNITS FOR SHORT AND LARGE LENGTHS :

Serial No.	Unit	Symbol	Meaning
1	fermi	f	10-15 m
2	angstrom	A0	10-10 m
3	Astronomical unit	AU	1.496 x1011 m (Average distance of the sun from earth )
4	light year	ly	9.46 x1015 m (distance that light travels with velocity of 3 x 108 m/s in one year )
5	parsec	parsec	3.08 x 1016 m (distance at which average radius of earth’s orbit subtends an angle of 1 arc second)

MEASUREMENT OF MASS :

• The unit used to measure mass of atoms or molecules is unified atomic mass unit (u). 1u = 1.66 x 10-27kg
• Mass of commonly available objects can be determined by a common balance.
• Large masses in the universe like planets, stars, etc., can be measured by using gravitational method.
• For measurement of small masses of atomic/subatomic particles etc., we make use of mass spectrograph.

MEASUREMENT OF TIME :

• To measure any time interval we need a clock.
• We now use an atomic standard of time, which is based on the periodic vibrations produced in a cesium atom- cesium clock or in general atomic clock.
• The cesium atomic clocks are very accurate.
• In our country, the NPL( National Physical Laboratory) has the responsibility of maintenance and improvement of physical standards, including that of time, frequency, etc.

DIMENSIONS

The powers to which the fundamental units of mass, length and time must be raised to represent the physical quantity are called the dimensions of that physical quantity.

For example:

Force = mass × acceleration

 = mass ×   = [MLT–2]

Hence the dimensions of force are 1 in mass 1 in length and (– 2) in time.

DIMENSIONAL FORMULA

Unit of a physical quantity expressed in terms of M, L and T is called dimensional formula. It shows how and which of the fundamental quantities represent the dimensions.

For example, the dimensional formula of work is [ML2T–2]

DIMENSIONAL EQUATION

When we equate the dimensional formula with the physical quantity, we get the dimensional equation.

For example : Work = [ML2T–2]

CLASSIFICATION OF PHYSICAL QUANTITIES (ON THE BASIS OF DIMENSIONS)

DIMENSIONAL FORMULA OF SOME IMPORTANT PHYSICAL QUANTITIES

SHORT CUTS / TIME SAVING TECHNIQUES

• To find dimensions of a typical physical quantity which is involved in a number of formulae, try to use that formula which is easiest for you. For example if you want to find the dimensional formula of magnetic induction then you can use the following formulae

Out of these the easiest is probably the third one.

• If you have to find the dimensional formula of a combination of physical quantities, then instead of finding the dimensional formula of each, try to correlate the combination of physical quantities with a standard formula. For example, if you have to find the dimension of CV2, then try to use formula

  

where E is the energy of a capacitor.

• 

velocity of light in vacuum

• Dimensions of the following are same

[ML2T–2]

• Dimensions of the following are same

Force = Impulse / time

= q v B = q E

= Thrust

=weight  = energy gradient  [MLT–2]

• The dimension of RC = is same as that of time

• Dimensions of the following are same

Velocity =     [M°LT–1]

• Dimensions of the following are same

Frequency   [M°L°T–1]

• Dimensions of the following are same

(E) Modulus of elasticity = Y (Young's modulus)

               = B (Bulk modulus)

   = η (Modulus of rigidity)

    = Stress

  = Pressure = [ML–1T–2]

• Dimensions of the following are same

Acceleration, retardation, centripetal acceleration, centrifugal acceleration, gravitational intensity/strength.       [M°LT–2]

• Dimensions of the following are same

Water equivalent, thermal capacity, entropy, Boltzmann's constant. [ML2T–2K–1]

POINTS TO REMEMBER

The dimensional formula of

• All trigonometric ratios are each  [M0L0T0]

• x in ex is [M0L0T0]

• ex is [M0L0T0]

• x in log x is [M0L0T0]

• log x is [M0L0T0]

ACCURACY AND PRECISION OF A MEASUREMENT :

• Accuracy of a measurement is a measure of how close the measured value is to the true value of the quantity.
• Precision is the resolution or limit with which the quantity is measured.
• The accuracy may depend on the limit or resolution of the measuring instrument.

ERRORS IN MEASUREMENT:

• Error is the uncertainty in a measurement.
• It is the difference between measured value and true value of the quantity.

TYPES OF ERRORS

• Errors can be classified as:

1. Systematic Errors
2. Random errors
3. Least count errors

Systematic errors

• The systematic errors are those errors that tend to be in one direction, either positive or negative.
• The sources of systematic errors are:

1. Instrumental errors - These errors arise from the errors due to imperfect design or calibration of the measuring instrument, zero error in the instrument, etc.
2. Imperfection: They also may arise  in experimental technique or procedure
3. Personal errors – They also may arise due to an individual’s wrong concept, bias, lack of proper setting of the apparatus or individual’s carelessness in taking observations without observing proper precautions, parallax error, etc.

Minimizing systematic errors

• Systematic errors can be minimized by

1. Improving experimental techniques
2. Selecting better instruments
3. Removing personal bias as far as possible.

Random errors

• These  errors occur less often , irregularly and are random with respect to sign and size of observed values.
• They arise due to random and unpredictable fluctuations in experimental conditions, unbiased personal errors etc.
• These  errors can be minimized by repeating the observations several times.

Least count errors

• Least count is the smallest value that can be measured by an instrument.

• Least count error is the error associated with the resolution of the instrument.
• Least count errors can be minimized by :

1. Using instruments of higher precision
2. Improving experimental techniques

ESTIMATION OF ERRORS :

• The arithmetic mean of all the observations in a measurement is taken as the true value of the quantity in the absence of any other method of  knowing the true value.
• For n observations a1, a2,a3,…..an , the true value of the quantity is given by the AM of the given data where AM is the Arithmetic Mean.

Absolute error ( |Δx| )

Absolute error is the magnitude of the difference between the true value of the quantity and the individual measurement value.

For n observations  x₁, x₂, x₃,…..xₙ , the absolute errors in the measured values are given by

The absolute error will be always positive.

Mean absolute error( Δamean)

• The arithmetic mean of all the absolute errors is taken as the final or mean absolute error of the value of the physical quantity.
• Thus the mean absolute error can be calculated as, 
  

• 
  

   

• Thus, any measured value can be written as

• That is any measurement ‘a’ of the physical quantity lies between                         amean + Δamean      and    amean − Δamean .
• Or, it can be written as (amean − Δamean) < a < amean +Δamean

Relative error :

• Ratio of the mean absolute error to the mean value of the quantity.

Percentage error (a)

• It is the relative error expressed in percentage.

Using least count, percentage error can be calculated as follows.

PROBLEM -1

We measure the period of oscillation of a simple pendulum. In successive measurements, the readings turn out to be 2.63 s, 2.56 s, 2.42 s, 2.71s and 2.80 s. Calculate the absolute errors, relative error or percentage error.

Solution

Given T1=2.63s, T2=2.56s, T3 =2.42 s, T4=2.71 s, T5=2.80 s .  

Mean period of oscillation

Absolute errors in the time period

Mean absolute error of time period

Thus, the period of oscillation of the pendulum lies between 2.62 + 0.11 and 2.62 – 0.11.or between 2.73 and 2.51.

Since the error is 0.11s , the value of time period can be written in a more correct way as

T = 2.6 ±0.1s

Relative error of time period

Percentage error

COMBINATION OF ERRORS :

Error of a sum or a difference

• When two quantities are added or subtracted, the absolute error in the final result is the sum of the absolute errors in the individual quantities.
• Thus, for two quantities A and B, the absolute error in the sum or difference will be

ΔZ = ΔA+ ΔB

Where ΔZ = absolute error in sum or difference

ΔA = absolute error in A

ΔB = absolute error in B

Proof

PROBLEM

The temperatures of two bodies measured by a thermometer are t1 = 20 0C ± 0.5 0C and t2 = 50 0C ± 0.5 0C. Calculate the temperature difference and the error in it.

Solution

• The temperature difference

Error of a product or a quotient

• When two quantities are multiplied or divided, the relative error in the result is the sum of the relative errors in the multipliers.
• Thus, for two quantities A and B, the relative error in the product or quotient will be

Proof

• For Z = AB, we may write

• Dividing LHS by Z and RHS by AB, we get

• Since ΔA and ΔB are small, we shall ignore their product.
• Thus, the maximum relative error is given by

• This is true for division also.

• By using binomial theorem

• Neglecting last term we get

PROBLEM

• The resistance R = V/I where V = (100 ± 5)V and I = (10 ± 0.2)A. Find the percentage error in R.

Solution

Percentage error in V is given by

Percentage error in I is

Thus percentage error in R

δR = 5% + 2% = 7%

Error in case of a measured quantity raised to a power

The relative error in a physical quantity raised to the power k is the k times the relative error in the individual quantity.

Thus, for Z = Ak , the relative error is given by

PROBLEM

Solution

SIGNIFICANT FIGURES

The number of digits, which are known reliably in our measurement, and one digit that is uncertain are termed as significant figures.

RULES TO DETERMINE THE NUMBERS OF SIGNIFICANT FIGURES

1. All non-zero digits are significant. 235.75 has five significant figures.

2. All zeroes between two non-zero digits are significant. 2016.008 has seven significant figures.

3. All zeroes occurring between the decimal point and the non-zero digits are not significant provided there is only a zero to the left of the decimal point.  0.00652 has three significant figures.

4. All zeroes written to the right of a non-zero digit in a number written without a decimal point are not significant. This rule does not work if zero is a result of measurement. 54000 has two significant figures whereas 54000m has five significant figures.

5. All zeroes occurring to the right of a non-zero digit in a number written with a decimal point are significant. 32.2000 has six significant figures.

6. When a number is written in the exponential form, the exponential term does not contribute towards the significant figures. 2.465 × 105 has four significant figures.

POINTS TO REMEMBER

• The significant figures depend upon the least count of the instrument.

• The number of significant figures does not depend on the units chosen.

ROUNDING OFF

• If the digit to be dropped is less than 5 then the preceding digit should be left unchanged.

• If the digit to be dropped is more than 5 then one should raise the preceding digit by one.

• If the digit to be dropped is 5 followed by a digit other than zero then the preceding digit is increased by one.

• If the digit to be dropped is 5 then the preceding digit is not changed if it is even.

• If the digit to be dropped is 5 then the preceding digit is increased by one if it is odd.

ARITHMETICAL OPERATIONS WITH SIGNIFICANT FIGURES AND ROUNDING OFF

• For addition or subtraction, write the numbers one below the other with all the decimal points in one line. Now locate the first column from the left that has a doubtful digit. All digits right to this column are dropped from all the numbers and rounding is done to this column.  Addition subtraction is then done.

Example : Find the sum of 23.623 and 8.7 to correct significant figures.

Sol.  Step-1 :- 23.623 + 8.7 

Step-2 :-  23.6 + 8.7=32.3

• In multiplication and division of two or more quantities, the number of significant digits in the answer is equal to the number of significant digits in the quantity, which has a minimum number of significant digits.

The insignificant digits are dropped from the result if they appear after the decimal point. They are replaced by zeroes if they appear to the left of the decimal point. The least significant digit is rounded off.

Example : 107.88 (5.S.F.) × 0.610 (3S.F.) =  65.8068  ≅  65.8(3S.F.)

ACCURACY, PRECISION OF INSTRUMENTS AND ERRORS IN MEASUREMENTS

Accuracy and Precision are two terms that have very different meanings in experimental physics. We need to be able to distinguish between an accurate measurement and a precise measurement. An accurate measurement is one in which the results of the experiment agree with the ‘accepted’ value.

Note:- This only applies to experiments where this is the goal like measuring the speed of light. A precise measurement is one that we can make to a large number of decimal places.

The following diagrams illustrate the meaning of terms accuracy and precision

In the above figure: The centre of the target represents the accepted value. The closer to the centre, the more accurate the experiment. The extent of the scatter of the data is a measure of the precision.

A - Precise and accurate

B - Accurate but imprecise

C - Precise but not accurate

D - Not accurate nor precise

When successive measurements of the same quantity are repeated there are different values obtained. In experimental physics it is vital to be able to measure and quantify this uncertainty. (The words "error" and "uncertainty" are often mistaken for one another by physicists ; although it is not ideal - but one has to get used to it!)

Error in measurements is the difference of actual or true value and measured value.

Error = True value – Measured value

Points To Remember

1. Accuracy depends on the least count of the instrument used for measurement.

2. In the addition and subtraction operation, the result contains the minimum number of decimal places of the figures being used

3. In the multiplication and division operation, the result contains the minimum number of significant figures.

4. Least count (L.C.) of Vernier callipers =  one MSD – one VSD

where MSD = mains scale division, VSD = Vernier scale division

5. Least count of screw gauge (or spherometer)
   where pitch is the ratio of number of divisions moved on linear scale and number of rotations given to circular scale.

6. Pure number or unmeasured value do not have significant numbers

7. Change in the position of a decimal does not change the number of significant figures. Similarly, the change in the units of measured value does not change the significant figures.

8. Accuracy of a measured value refers to how close a measurement is to the correct value. The uncertainty in a measurement is an estimate of the amount by which the measurement result may differ from this value.

9. Precision of measured values refers to how close the agreement is between repeated measurements.

10. The precision of a measuring tool is related to the size of its measurement increments. The smaller the measurement increment, the more precise the tool.

11. Significant figures express the precision of a measuring tool.

12. When multiplying or dividing measured values, the final answer can contain only as many significant figures as the least precise value.

13. When adding or subtracting measured values, the final answer cannot contain more decimal places than the least precise value.

COMMON ERRORS IN MEASUREMENTS

It is not possible to measure the 100% correct value of any physical quantity, even after measuring it so many times. There always exists some uncertainty, which is usually referred to as experimental error.

EXPERIMENTAL ERRORS

Random error: It is the error that has an equal chance of being positive or negative.

It occurs irregularly and at random in magnitude and direction. It can be caused

• by the lack of perfection of observer

• if the measuring instrument is not perfectly sensitive.

Systematic error:  It tends to occur in one direction either positive or negative. It occurs due to

• measuring instrument having a zero error.

• an instrument being incorrectly calibrated (such as slow- running-stop clock) or with a faulty alignment.

• the observer persistently carrying out a mistimed action (wrong timing in starting and stopping a clock)

For measuring a particular physical quantity, we take a number of readings. Let the readings be X1, X2............,Xn. Then the mean value is found as follows

METHODS OF EXPRESSING ERROR

Absolute error :  It is the difference between the mean value and the measured value of the physical quantity.

|ΔX1|  = |Xmean–X1|  

..................................

..................................

|ΔXn|  = |Xmean–Xn|  

Mean absolute error:

ΔXmean or =

Relative error : It is the ratio of the mean absolute error and the value of the quantity being measured.

Percentage error : It is the relative error expressed in percent

Percentage error

TO FIND THE MAXIMUM ERROR IN COMPOUND QUANTITIES

SUM AND DIFFERENCE

We have to find the sum or difference of two values given as (a ± Δa) and (b ± Δb), we do it as follows

X ± ΔX = (a ± Δa) + (b ± Δb) = (a + b) ± (Δa + Δb)

⇒ X = a + b and ΔX = Δa + Δb in case of sum

And X = (a – b) and ΔX = Δa + Δb in case of difference.

PRODUCT AND QUOTIENT

We add the fractional or percentage errors in case of finding product or quotient.

If P = ab then

If  then

POWER OF A QUANTITY

If  x = an , then

 

Example:   

For, If and

Then × 100 = (2 × 3 + 4)% = 10%

Similarly:

Points To Remember

1. More the accuracy, the smaller the error.

2. Absolute error |ΔX| is always positive.

3. |ΔX| has the same dimensions as that of X.

4. If the least count of the measuring instrument is not given and the measured value is given the least error in the measurement can be found by taking the last digit to be 1 and the rest digit to be zero. For e.g. if the measured value of mass m = 2.03 kg then.

5. If a number of physical quantities are involved in an expression then the one with higher power contributes more in errors and therefore should be measured more accurately.

6. Relative error is a dimensionless quantity.

7. We are always interested in calculating the maximum possible error.

SIGNIFICANT FIGURES

• The number of digits in a measurement about which we are certain and one additional digit which is uncertain is known as significant figures.

• The number of significant figures indicates the accuracy with which the quantity is measured.

RULES FOR DETERMINING SIGNIFICANT FIGURES

•    All the non-zero digits are significant and the zeros between the nonzero digits are significant. 

       Example : In 1.20005 there are 6 significant figures.

•     If the number is less than 1, the zero(s) on the right of decimal point but to the left of the first non-zero digit are not significant. 

             Example : In 0.00005207, the underlying zeroes between decimal point and 5 are not significant. So it would have 4 significant figures.

•    The terminal or trailing zero(s) in a number without a decimal point are not significant. 

              Example : Thus 357 m = 35700 cm = 357000 mm has three significant figures, the trailing zero(s) being not significant.

•    The trailing zero(s) in a number with a decimal point are significant. 

            Example : The numbers 2.700 or 0.03800 have four significant figures each.

PROBLEM

• State the number of significant figures in the following:

1. a) 0.007m2 b) 2.64 x 1024 kg c) 0.2370 g cm-3

d) 6.320 J e) 6.032 Nm-2 f) 0.0006032 m2.

Solution

a)1   b) 3   c) 4   d) 4   e) 4   f) 4

Scientific Notation

• In this notation, every number is expressed as a x 10b.
• where a is a number between 1 and 10, and b is any positive or negative exponent (or power) of 10.

Order of magnitude of a physical quantity :

• in scientific notation, to get an approximate idea of the number, we may round off the number a to 1 (for a ≤ 5) and to 10 (for 5<a ≤ 10).
• Then the number can be expressed approximately as 10b in which the exponent (or power) b of 10 is called order of magnitude of the physical quantity.
• For example, the diameter of the earth (1.28×107m) is of the order of 107m with the order of magnitude 7.

Rules for arithmetic operation with significant figures Multiplication / Division

• In multiplication or division, the final result should retain as many significant figures as are there in the original number with the least significant figures.

Addition or subtraction

• In addition or subtraction, the final result should retain as many decimal places as are there in the number with the least decimal places.
• For example,

436.32 g + 227.2 g + 0.301 g = 663.821 g = 663.8 g.

Rounding off the uncertain digit

• If the insignificant digit to be dropped is more than 5 preceding digit is raised by 1
• Eg : 1.68 =1.7 to 2 significant figures
• If the insignificant digit to be dropped is less than 5. it is left unchanged.
• Eg: 1.62=1.6 to 2 significant figures .

If the insignificant digit is 5:

• if the preceding digit is even, the insignificant digit is simply dropped and if it is odd, the preceding digit is raised by 1.

Eg: 2.745 =2.74 and 2.735 =2.74

PROBLEM-1

• Each side of a cube is measured to be 7.203 m. What are the total surface area and the volume of the cube to appropriate significant figures?

Solution

• The number of significant figures in the measured length is 4. The calculated area and the volume should therefore be rounded off to 4 significant figures.
• Hence, Surface area will be calculated as                                                                                        S= 6 x (7.203)2 = 311.299254m2 = 311.3m2

• Volume will be calculated as                                                                                                          V=(7.203)3 = 373.714754m3 = 373.7m3

PROBLEM -2

If the length and breadth of a thin rectangular sheet are measured, using a meter scale as 16.2 cm and 10.1 cm respectively. Express length and breadth in proper error limits. Also calculate area of the rectangular sheet with error limits.

Solution

• The least count of the meter scale = 0.1 cm, this will be equal to the absolute error (Δl).
• Thus, length can be expressed as

l =16.2 ± 0.1cm

• The percentage error in length can be calculated as

• So, length can also be written as

l =16.2cm ± 0.6%

• Similarly, breadth can be written as

63.62 1.6% 2 A or b =10.1cm ±1%

• Area is given by

A = l x b = 163.62cm2 ± 1.6% or A = 163.62 ± 2.6cm2

• In proper significant figures ,area

A = 164 ± 3cm2

DIMENSIONAL ANALYSIS AND ITS APPLICATIONS

Principle of Homogeneity: Only those physical quantities can be added /subtracted/equated /compared which have the same dimensions. This principle has a very wide application in dimensional analyses.

It states that, “The dimensional formula of each term on both the sides of a correct formula remains the same.”

For example, If S= ut+1/2at2 is a correct formula, then the three terms S, ut and 1/2at2 should have the same dimensional formula.

USES OF DIMENSIONS

Dimensional Analysis is chiefly employed for three purposes, three C’s namely Conversion, Correction and Correlation.

1. Conversion of one system of unit into another

Example: Convert a pressure of 106 dyne/cm2 in S.I units.

Sol. We know that 1N = 105 dyne ⇒ 1 dyne = 10–5 N

Also, 1m = 100 cm ⇒ 1 cm = 10–2 m

Now, the pressure 106 dyne/cm2 in SI unit is

2. Checking the accuracy of various formulae

Example : Check the correctness of the following equation dimensionally

where F = force, η = coefficient of viscosity, A = area, gradient w.r.t distance, θ = angle of contact

Sol. L.H.S = force = [MLT–2]

R.H.S =

The equation is dimensionally correct.

3. Derivation of formula

Example: The air bubble formed by explosion inside water performed oscillation with time period T which is directly proportional to Pa db Ec where P is pressure, d is density and E is the energy due to explosion. Find the values of a, b and c.

Sol.  Let us assume that the required expression for time period is T = K Pa db Ec

where K is a dimensionless constant.

Writing dimensions on both sides,

Equating the powers,

a + b + c = 0 ....(1)

– a –3b + 2c = 0 ....(2)

– 2a – 2c = 1 ....(3)

Solving these equations,  we get,

a = , b = , c = .

LIMITATIONS OF DIMENSIONAL ANALYSIS

• No information about the dimensionless constant is obtained during dimensional analysis

• Formula cannot be found if a physical quantity is dependent on more than three physical quantities.

• Formula containing trigonometrical /exponential function cannot be found.

• If an equation is dimensionally correct it may or may not be absolutely correct.

DIMENSIONS OF PHYSICAL QUANTITIES

• All the physical quantities represented by derived units can be expressed in terms of some combination of seven fundamental or base quantities.
• The dimensions of a physical quantity are the powers (or exponents) to which the base quantities are raised to represent that quantity.
• Length has the dimension [L], mass [M], time [T], electric current [A], thermodynamic temperature [K], luminous intensity [cd], and amount of substance [mol].
• In mechanics, all the physical quantities can be written in terms of the dimensions [L], [M] and [T].

Dimensional formulae

• The expression which shows how and which of the base quantities represent the dimensions of physical quantity is called the dimensional formula of the given physical quantity.
• It appears in the form : 
  
  
  
• For example, the dimensional formula of the Force is 
  
  
  

Dimensional equation

• An equation obtained by equating a physical quantity with its dimensional formula is called the dimensional equation of the physical quantity.
• For example, the dimensional equations of volume [V], speed [v], acceleration [a], mass density [ 𝞺] force [F ] and pressure [p] may be expressed as

APPLICATIONS OF DIMENSIONAL ANALYSIS

• Dimensional analysis can be used in three important processes (CCC) :

a) Correction: To check the dimensional consistency of equations

b) Conversion: To convert a Physical quantity from one system to another.

c) Correlation :To deduce relation among physical quantities.

a) Correction: To check the dimensional consistency of equations or to check for correctness of an equation.

• The principle of homogeneity is used to check the dimensional correctness of equations.

Principle of homogeneity :
It states that the dimensional formula of each term  on both the sides of a correct formula is the same.

It means :

• The magnitudes of physical quantities may be added together or subtracted from one another only if they have the same dimensions.
• The equation L X = M Y +N Z , is dimensionally correct only if [LX] = [MY] = [NZ].

PROBLEM

• Check the dimensional consistency of the equation v = u + at .

Solution

We have , [v] = [M0LT-1]

[u] = [M0LT-1]

[at] = [M0LT-2] [ T] =[M0LT-1]

As  [v] =[u] =[at] , the equation is  correct dimensionally.

b) Conversion: To convert a Physical quantity from one system to another.

Problem :

What will be  the Potential Energy of a body of mass 300 kg placed at a height of 150 m against acceleration of gravity 9.8 m/s²  measured in a system where mass, length and time are measured in the units as 10 kg, 100 m and 10 s .  

Solution :

• The Potential Energy of a body is  the product of mass(m), acceleration due to gravity (g) and height (h).

• The dimensional formula of P.E. is found as follows :

•    The dimensional coefficients a, b, c are found to be 1, 2, -2.

The formula for conversion looks like:

• Finding  n₁ using the formula for P.E.,

        Hence  n₁=441000

• Now, putting the values, we get 

c) Correlation :To deduce relation among physical quantities

• For this we should know dependence of the physical quantity on other quantities and consider it as a product type of the dependence.

Problem :

Derive an expression for the Time Period T of a Simple pendulum in which a metal bob of mass m oscillates freely about its mean position from an inextensible massless string of length l under the action of gravity g.  

• The Time period of oscillation of the simple pendulum is found to depend on its length (l), mass of the bob (m) and acceleration due to gravity (g).
• The dependence of Time period T on the three quantities l, m and g as a product may be written as :
  
  
  
• Where k is a dimensionless constant ,   
                      

• Taking dimensions on both sides

• On equating the dimensions on both sides, we get

Putting the above values in the equation, we get  

This is the required expression for the Time period of a Simple pendulum.

Limitations of dimensional analysis

• The dimensional consistency does not guarantee correct equations.
• The arguments of special functions, such as the trigonometric, logarithmic and exponential functions are dimensionless.
• A pure number, ratio of similar physical quantities, such as angle as the ratio (length/length), refractive index as the ratio (speed of light in vacuum/speed of light in medium) etc., has no dimensions.
• Dimensionless constants cannot be obtained by this method.
• If an equation fails consistency test, it is proved wrong, but if it passes, it is not proved right.
• It does not distinguish between the physical quantities having same dimensions.

Additional Worksheets

 

Very Short Answer Questions (1 Mark Questions)

1. Define the S.I. Solid Angle Unit.

Ans. The steradian is the SI unit for solid angles. The angle formed by a spherical plane of unit square metre area in the centre of a sphere with a radius of unit length is defined as one steradian.

2. Name physical quantities using Electron Volt and Pascal as their units.

Ans. Energy and pressure are physical quantities with electron volt and pascal units, respectively.

3. What is the measurement unit for sound amplitude?

Ans. Decibel. A decibel is one-tenth of a bel, and it is a unit of the intensity of  Sound.

4. Is a mile the same on land as it is at sea?

Ans. A land mile or a statute mile is 5,280 feet long (1,609 meters) while  a mile on the water called a nautical mile is 6,076 feet long and is used on the ocean (1,852 meters). 

5. What is the definition of an acre?

Ans. An acre is a measurement unit for land area. The term acre comes from the Old English word acre, which means "a field." The acre was traditionally defined as the area that a yoke of oxen could plough in a day. The area of one acre is 43,560 square feet (4,840 square yards). A hectare is equal to 0.4047 acres (4,047 square meters).

6. What is the definition of horsepower?

Ans. Horsepower is a measurement of the force exerted by a horse when it pulls something. Engine and motor output is often referred to as "horsepower," which is a unit of measurement for power (or rate of work).  It is approximately 746 Watts.

7. What is the definition of the metric system?

Ans. The decimalized metric system is a decimalized measuring system.

The metre, gram, and litre are the three most popular basic units in the metric system.

 

Short Answer Questions (2 Marks Questions)

1. Describe the given data with brevity.

I. Science requires precise measurements of physical quantities. To determine an aircraft's speed, for example, a precise technique of determining its locations at closely spaced instants of time is required. This was the driving force for the development of radar during World War 

II. Consider a variety of situations in modern research when exact measurements of length, time, mass, and other variables are required. Also, wherever possible, provide a quantitative estimate of the accuracy required.

Ans.  Precise measurement is quite essential for the advancement of science,. Time intervals are measured using an ultra-short laser pulse. The interatomic separation is determined using X-ray spectroscopy. The mass spectrometer was designed to determine the mass of individual atoms.

2. Explain the frequent observation with clarity.

 While looking out the window of a fast-moving train, close trees, homes, and other things appear to move swiftly in the opposite direction of the train, yet distant objects (hilltops, the Moon, the stars, and so on) appear to remain immobile. (And these distant things appear to move with you because you are aware that you are moving.)

Ans. The line of sight is a virtual line that links the observer's eye to the object. When we look at items very close , we observe that they move swiftly in the other way when the line-of-sight shifts. The distant objects, on the other hand, appear to be immobile since the line of sight does not shift fast.

3. Peter is 48000 grams in weight. How much does he weigh in kilograms?

Ans. Peter's weight is 48000 grams . Kilograms and grams are both measuring units, and we divide the amount by 1000 to convert grams to kilograms.

1/1000 kg = 1 g

48000 g = 48000/1000 kg

= 48 kg

Hence, Peter's weight is 48 kg.

4. Lara covers 1.5 miles every day on her bicycle. In a week, how many kilometres does she ride?

Ans. A mile is 1.6 kilometres long. Multiply 1.5 miles by 1.6 kilometres to convert miles to kilometres.(Since 5 miles are 8 Kilometers)

1 mile equals 1.6 kilometres

1.5 miles = 1.5 × 1.6 kilometres

= 2.4 kilometres

So, in  7 days in a week, Lara would ride a distance of

= 7 × 2.4 km  

= 16.8 kms

Hence Lara rides 16.8 kilometres every week .

 

5. Two cesium clocks, if left to operate for 100 years without being disturbed, are said to differ by only 0.02 seconds. What does this mean for the precision of a conventional cesium clock in measuring a one-second interval?

Ans. Total time = 100 years = 100 × 365 × 24 × 60 × 60 s

In 100 years, the error is 0.02 seconds.

In 1 second, there was an error = 0.02/100 × 365 × 24 × 60 × 60

= 6.34 × 10-12 s

Hence, the precision of a conventional cesium clock in measuring a one-second interval is 10-12 seconds.

6. A grocer's balance measures the mass of a box at 2.30 kg. The box now contains two gold pieces with weights of 20.65 g and 20.73 g. What is?

(a) the box's overall weight,

(b) the mass difference between the two pieces in order to rectify significant figures?

Ans.(a) The package weighs 2.70 kg. (Significant Figures=3)

and the first gold piece weighs 20.65 grams= 0.2065 kg

The second gold piece weighs 20.73 grams = 0.2073 kg

The total mass = 2.300 + 0.2065 + 0.2073 = 2.7138 kg

Because the first measurement 2.30 Kg has the fewest decimal points, the total mass equals 2.71 kg.(Significant Figures=3)

(b) The mass difference is 0.08 g (20.73g – 20.65 g = 0.08 g.)

The  mass difference equals 0.08 g since 2 is the smallest number of decimal places.

7. (a) A thread and a metre scale are handed to you. How will you determine the thread's diameter?

(b) A screw gauge features a circular scale with 200 divisions and a pitch of 1.0 mm. Do you believe that increasing the number of divisions on the circular scale may arbitrarily enhance the screw gauge's accuracy?

(c) Vernier callipers are used to determine the average diameter of a thin brass rod. Why is it assumed that a set of 100 diameter measurements will produce a more trustworthy estimate than a set of only 5 measurements?

Ans. (a) Wrap the thread around a pencil many times to produce a coil with the twists close together. Now, using a metre scale, determine the length of this coil. The diameter of the thread is provided by the relationship Diameter = L/n, where L is the length of the coil and n is the number of turns of the coil.

(b) The screw gauge's least count is equal to the pitch divided by the number of divisions on the circular scale.

Now, as a result, increasing the number of divisions on the circular scale should reduce the screw gauge's least count. As a consequence, the accuracy of the screw gauge will increase. However, this is simply a hypothesis. When the number of turns is raised, there will be many more challenges.

(c) In 100 observations, the likelihood of committing random mistakes is lowered to a greater extent than in 5 observations.

 International System of Units

 

Long Answer Questions (3 Marks Questions)

1. Ultrasonic waves are used by a SONAR (sound navigation and ranging) to identify and locate items underwater. The time delay between the creation of a probe wave and the receiving of its echo after reflection from an enemy submarine is determined to be 77.0 seconds in a submarine equipped with a SONAR. What is the hostile submarine's distance? (In water, the speed of sound is 1450 m s–1).

Ans. v = 1450 m s–1 is the speed of sound in water.

2t = 77.0 s is the time between creation and receipt of the echo after reflection

t = 77.0/2 = 38. 5 s is the time it takes for sound waves to reach the submersible.

We know, v = d/t 

d = tv, enemy's submarine distance

As a result, d = v × t = (1450 × 38. 5) = 55825 m = 55.8 × 103 m or 55.8 km is calculated.

2. It is well known that during a total solar eclipse, the moon's disc almost fully covers the Sun's disc. Determine the moon's approximate diameter.

Ans. The Moon's distance from Earth is 3.84 × 108 metre.

The Sun's distance from the Earth is 1.496 × 1011 metre.

The diameter of the sun is 1.39 × 109 m.

The angular diameter of the Sun is = 1920′′ = 1920 × 4.85 × 10-6 rad 

= 9.31 × 10-3 rad. [1-inch equals 4.85 × 10-6 rad]

Because the moon's disc fully covers the sun's disc during a total solar eclipse, both the sun and the moon must have the same angular diameter.

As a result, the moon's angular diameter θ is 9.31 × 10-3 rad.

S = 3.8452 × 108 m is the earth-moon distance.

As a result, D = θ × S= 9.31 × 10-3 × 3.8452 × 108 m = 35.796 × 105 m is the moon's diameter.

 

3. Calculate the average mass density of a sodium atom with a size of 2.5 as a starting point. (Use the known Avogadro's number and sodium atomic mass values.) When you compare it to the mass density of sodium in its crystalline form, you will notice a significant difference: 970 kg m–3 Is the order of magnitude of the two densities the same? If so, what is the reasoning behind it?

Ans. 2.5𝚨⁰ = 2.5 × 10-10 m is the diameter of sodium.

As a result, the radius is 1.25 × 10-10 metre.

V = (4/3)𝝅r3 is the volume of a sodium atom.

= (4/3) × (22/7) × (1.25 × 10-10) 3= 8.177 × 10-30 m3

One mole atom of sodium has a mass of 23 g = 23 × 10-3 kg.

6.023 × 1023 atoms make up one mole of sodium.

As a result, M = 23 × 10-3  kg/6.023 × 1023 = 3.818 × 10-26 kg is the mass of one sodium atom.

Therefore,

Atomic mass density of sodium

M/V = 3.818 × 10-26 kg/8.177 × 10-30 m3 

= 4669.2 kg m-3 = 0.46692 × 104 kg m-3

The density of sodium in solid state is 4669.2 kg m-3,whereas it is 970 kg m-3 in the crystalline phase. As a result, they are in a different order. Atoms are closely packed in the solid state, but in the crystalline state, they organize themselves in a void-filled sequence. Thus, as an outcome, the density of the solid phase is larger than that of the crystalline phase.

 

4. The Sun is a heated plasma (ionized matter) with a temperature of over 107 K in its inner core and over 6000 K on its outer surface. No material can exist in a solid or liquid state at these temperatures. In terms of densities of solids, liquids, and gases, where do you think the Sun's mass density will fall? Check the following data to see whether your assumption is correct: The Sun has a mass of 2.0 × 1030 kilograms and a radius of 7.0 × 108 metre.

Ans. Mass = 2 × 1030 kg

Radius = 7 × 108 m
Volume, $V=\frac{4}{3}𝝅r^3$

$=\frac{4}{3}\times \frac{22}{7}\times (7\times {10}^8{)}^3$

$=\frac{88}{21}\times 343\times {10}^{24}{m}^3$

= 1437.33 × 1024 m3

Density = $\frac{\text{Mass}}{\text{Volume}}=\frac{2\times {10}^{30}}{1437.3\times {10}^{24}}=1.39\times {10}^{3}kg/m^3$

The density falls in between solids and liquids. Its density is owing to the sun's inner layer's strong gravitational influence on the outer layer.

 

Very Long Answer Questions (5 Marks Questions)

1. In a test to determine the size of an oleic acid molecule In 19 mL of alcohol, 1 mL of oleic acid is dissolved. Then, using alcohol, dilute 1 mL of this solution to 20 mL. Now, 1 drop of this diluted solution is dropped into a shallow trough of water. The solution forms a one-molecule thick film on the water's surface. The film is now uniformly dusted with lycopodium powder, and its diameter is measured. We can compute the thickness of the film using the volume of the drop and the area of the film, which will give us the size of the oleic acid molecule.

Answer the following questions after carefully reading the passage:

1. Why is oleic acid dissolved in alcohol?
2. What role does lycopodium powder play?
3. How much oleic acid would be in each mL of the solution prepared?
4. In what way will you determine the volume of n drops of oleic acid solution?
5. How much oleic acid will be in one drop of this solution?

Ans. (a) Oleic acid is dissolved in alcohol since it does not dissolve in water.

(b) When uniformly dusted, lycopodium powder covers the whole surface of the water.

Oleic acid does not dissolve in water when a drop of the prepared solution is placed on it. Instead, it spreads over the water's surface, pushing the lycopodium powder away from the drop's landing place. As a result, we can calculate the area covered by oleic acid.

(c) The volume of oleic acid in each mL of the solution made = $\frac{1}{20}$mL × $\frac{1}{20}$ = $\frac{1}{400}$mL

(d) A burette and measuring cylinder may be used to compute the volume of n droplets of this oleic acid solution, and the number of drops can be counted.

(e) If n drops of the solution equal 1 mL, the amount of oleic acid in one drop is $\frac{1}{\left(400\right)n}$  mL.

2. (a) One parsec equals how many astronomical units (A.U.)?

(b) The diameter of the Sun is nearly 400 times  that of the Earth and the diameter of Mars is roughly half that of the Earth. It is roughly 1/2 A.U. from the earth when it is closest to it. Calculate the size of it as viewed through the same telescope.

Ans. (a) 

(b )  

From a distance of  1 A.U., the Sun seems to be 1/2 degree in diameter, while Mars appear to be 1/1600 degree in diameter.

Mars will seem to be 1/800 degree in diameter at 1/2 A.U. 

With a magnification of 100, Mars seems to be 1/8-degree =60/8 arc min = 7.5   arc min.

Due to atmospheric variations, this exceeds the resolution limit. As a result, it seems to be exaggerated.

3. (a) Demonstrate that 1 u has an energy equivalent of 931.5 MeV.

(a) Sonu  writes 1 u = 931.5 MeV as the relation. Her teacher points out that the relationship is erroneous in terms of dimensions. Fill in the missing information.

Ans. Given:

m = 1

u = 1.67 × 10-27 kg

c = 3 × 108 m/s

According to the formula, E = mc2

E = 1.67 × 10-27 × 3 × 108 × 3 × 108  J 

= 1.67 × 10-27+8+8 × 9 J

$=\frac{\left(1.67\right)\left(9\right)\left({10}^{-11}\right)}{\left(1.6\right)\left({10}^{-13}\right)}$    MeV

= 939.4 MeV

≅ 931.5 MeV

(b) 931.5 MeV will release 1 u mass converted to total energy.

1 a.m.u. = 931.5 MeV, on the other hand, is dimensionally wrong.

As E = mc2 and we have mass = 1u,  

So, 1 uc2 ≅ 931.5 MeV, will be dimensionally correct.